In this short post I will backtest buy on gap intraday mean reversion strategy and demonstrate how its performance has deteriorated over time. The strategy is described in E.P.Chan’s book ‘Algorithmic trading: winning strategies and their rationale’. The rules of the strategy are very simple, below is a quote from the book describing it:
1. Select all stocks near the market open whose returns from their previous day’s lows to today’s opens are lower than one standard deviation.The standard deviation is computed using the daily close- to-close returns of the last 90 days.These are the stocks that “gapped down.”
2. Narrow down this list of stocks by requiring their open prices to be higher than the 20-day moving average of the closing prices.
3. Buy the 10 stocks within this list that have the lowest returns from their previous day’s lows. If the list has fewer than 10 stocks, then buy the entire list.
4. Liquidate all positions at the market close.
As my stock universe I will use constituent stocks of Vanguard Small-Cap Value ETF (ticker: VBR). The list of constituent stocks might not be exactly accurate because I parsed it several months ago, but it not important. The main goal is to have big enough stock universe. I used small-cap stocks because I think that small-cap market should be less efficient and therefore have more trading opportunities compared to large-cap stocks from SP500. Also we need to understand that the data used has a survivorship bias, but since our holding period is from market open to market close, it shouldn’t matter.
I will backtest the strategy using 3 year periods starting in 2005 and moving 1 year forward until 2018. I will remove any stocks that has a volume of less than 1000 on any trading day during the backtest period. I assume that two-way transaction cost is 0.1%. The code for backtesting is provided below.
| std_win = 90 # moving window for standard deviation | |
| ma_win = 20 # moving window for the mean | |
| starts = np.arange(2005,2019) # start years | |
| length = 3 # 3 year periods | |
| tc = 0.001 # 0.1% two-way transaction cost | |
| all_cumret = {} | |
| all_cumret_tc = {} | |
| market_cumret = {} | |
| num_stocks = {} | |
| for start in starts: | |
| # set start and end dates | |
| start_date = f'{start}-01-01' | |
| end_date = f'{start+length-1}-12-31' | |
| # prepare data | |
| prices_open = pd.read_csv('vbr99_21_open.csv', index_col=0) | |
| prices_high = pd.read_csv('vbr99_21_high.csv', index_col=0) | |
| prices_low = pd.read_csv('vbr99_21_low.csv', index_col=0) | |
| prices_close = pd.read_csv('vbr99_21_close.csv', index_col=0) | |
| volume = pd.read_csv('vbr99_21_volume.csv', index_col=0) | |
| prices_open = prices_open.loc[start_date:end_date].dropna(axis=1) | |
| prices_high = prices_high.loc[start_date:end_date].dropna(axis=1) | |
| prices_low = prices_low.loc[start_date:end_date].dropna(axis=1) | |
| prices_close = prices_close.loc[start_date:end_date].dropna(axis=1) | |
| volume = volume.loc[start_date:end_date].dropna(axis=1) | |
| # drop stocks with volume<1000 at any trading day | |
| low_vol = (volume<1000).sum() | |
| low_vol_symbols = low_vol[low_vol!=0].index | |
| prices_open.drop(low_vol_symbols, axis=1, inplace=True) | |
| prices_high.drop(low_vol_symbols, axis=1, inplace=True) | |
| prices_low.drop(low_vol_symbols, axis=1, inplace=True) | |
| prices_close.drop(low_vol_symbols, axis=1, inplace=True) | |
| num_stocks[start] = len(prices_open.columns) | |
| # calculate returns | |
| returns_close = prices_close.pct_change().dropna() # daily close-to-close returns | |
| returns_low_open = prices_open / prices_low.shift() - 1 # today open over previous day close | |
| returns_open_close = prices_close / prices_open - 1 # today close over today open | |
| # calculate moving average and moving std | |
| ret_close_std = returns_close.rolling(std_win).std() | |
| prices_close_ma = prices_close.rolling(ma_win).mean() | |
| # drop NA and align indexes | |
| ret_close_std = ret_close_std.dropna() | |
| prices_close_ma = prices_close_ma.loc[ret_close_std.index] | |
| returns_close = returns_close.loc[ret_close_std.index] | |
| returns_low_open = returns_low_open.loc[ret_close_std.index] | |
| returns_open_close = returns_open_close.loc[ret_close_std.index] | |
| prices_open = prices_open.loc[ret_close_std.index] | |
| # find stocks satisfying required conditions | |
| candidates = ((returns_low_open < ret_close_std) & (prices_open > prices_close_ma)) | |
| # prepare dataframe for storing strategy returns | |
| algo_returns = pd.DataFrame(index=candidates.index, columns=['return']) | |
| # backtest | |
| for t in candidates.index: | |
| # stocks satisfying required conditions | |
| candidates_today = candidates.loc[t][candidates.loc[t]==1].index | |
| # up to 10 stocks chosen for trading | |
| symbols = returns_low_open.loc[t][candidates_today].sort_values().index[:10] | |
| # end of day returns | |
| ret = returns_open_close.loc[t][symbols].sum() / len(symbols) | |
| algo_returns.loc[t]['return'] = ret | |
| # calculate cumulative returns | |
| all_cumret[start] = (algo_returns+1).cumprod().fillna(method='ffill') # without transaction costs | |
| all_cumret_tc[start] = (algo_returns+1-tc).cumprod().fillna(method='ffill') # with transaction costs | |
| market_cumret[start] = (returns_close.mean(axis=1) + 1).cumprod().fillna(method='ffill') |
Now let’s look at the results.
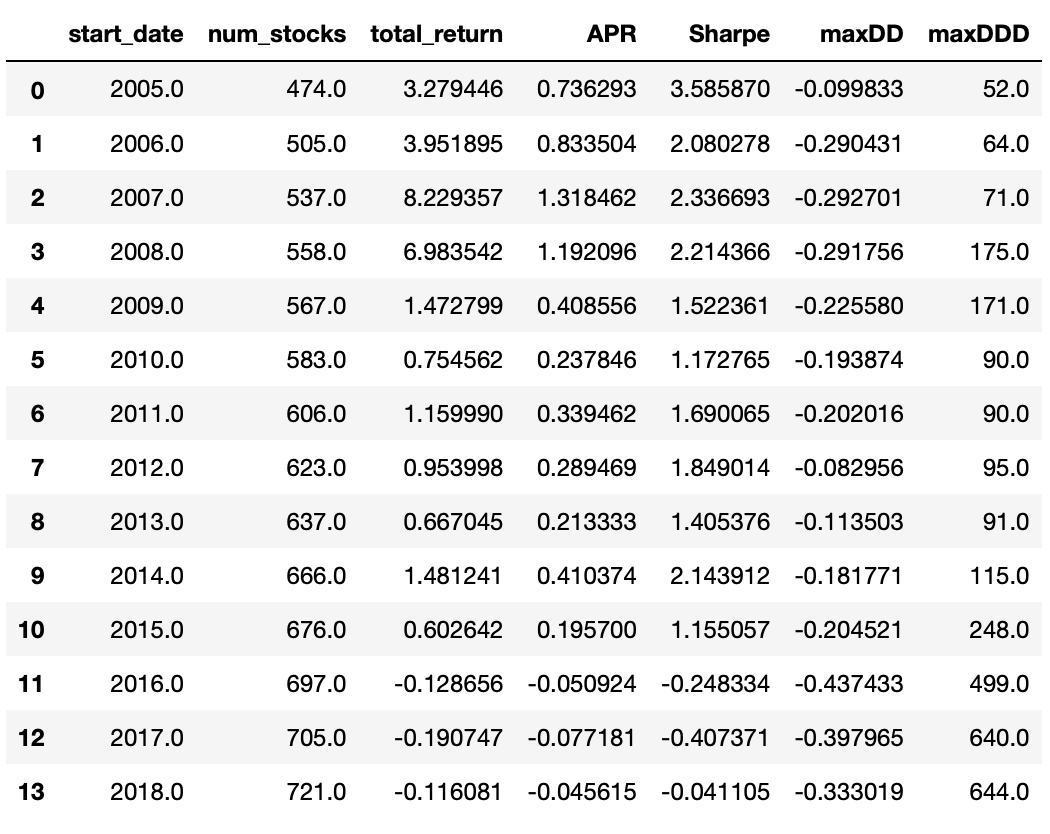
As we can see above the strategy has very good performance in earlier time frames. Sharpe ratio for a 3-year period starting in 2005 is 3.58 and the strategy continues to have positive returns and Sharpe ratio bigger than one until 2015–2018 trading period. Now let’s look at the results which account for the transactions costs.
Here the returns and Sharpe ratios are significantly lower, but they are still very good in earlier time frames. In 2008–2011 trading period strategy’s Sharpe ratio is 1.57 with an APR of 70%. But then the performance starts to deteriorate. The book was published in 2013 and after that time only one period (2014–2017) has positive returns. Let’s look at the scatter plot of Sharpe ratios.
We can clearly see a downward trend in Sharpe ratios on the plot above. Now I will plot strategy returns for the first (2005–2008) and the last (2018–2021) trading periods. Also for comparison I will include market returns (average return of all stocks during that period).
Here we have clearly demonstrated how performance of buy-on-gap strategy has deteriorated over time. I was surprised to see how well this simple strategy performed in 2005–2010. I think it might be interesting to test this strategy on different (non-US) markets or maybe experiment with different lengths of moving windows used for calculating moving average and moving standard deviation.
Jupyter notebook with source code is available here.
If you have any questions, suggestions or corrections please post them in the comments. Thanks for reading.