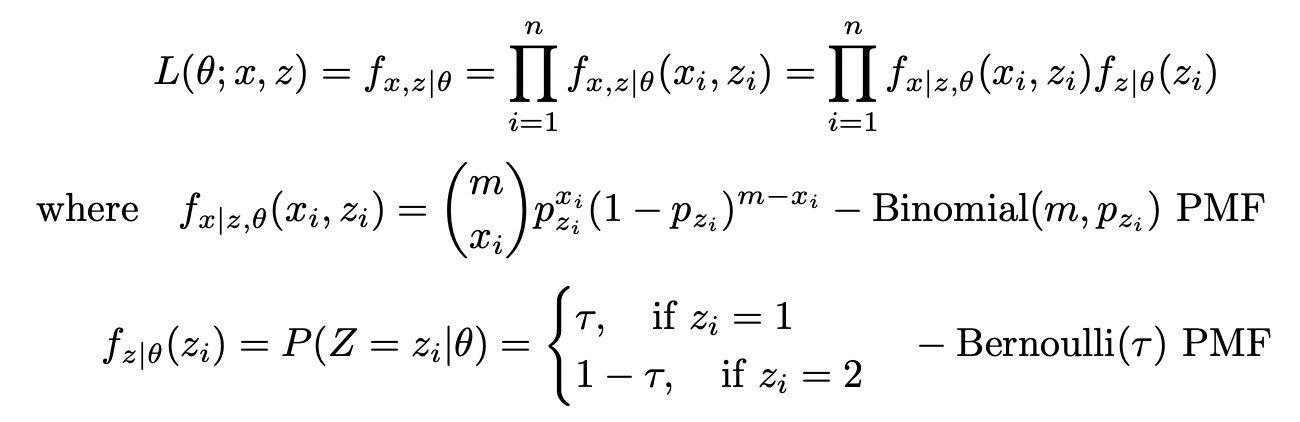Introduction to Expectation Maximization algorithm

A framework for estimating parameters with incomplete data.

Aug 07, 2024

Expectation Maximization (EM) algorithm is widely used for estimating parameters of different statistical models. It is an iterative algorithm that allows us to break one difficult optimization problem into several simpler optimization problems. In this article I will explain how it works on several simple examples.

Probably the most popular example of this algorithm (the most discussed on the internet) comes from this paper. It’s a very simple example but I think it is good to start with basics.

Assume we have two coins (coin 1 and coin 2) with differrent probabilities of getting heads. We choose one of the coins, make m=10 flips and record the number of heads. Let’s say we repeat this experiment n=5 times. Our task is to determine the probability of getting heads for each coin. We have:

First assume that we know which coin was used in each experiment. In that case we have complete information and can easily solve for p_1 and p_2using maximum likelihood estimation (MLE) technique. We begin by calculating likelihood function and taking its logarithm (because it’s easier to maximize log-likelihood function). Since we have n independent experiments, likelihood function is just a product of individual probability mass functions (PMF) evaluated at x_i (number is heads in experiment i).

Now we need to maximize log-likelihood function with respect to probabilities p_1 and p_2. It can be done either numerically or analytically. I will demonstrate both methods. First let’s solve it analytically. We can solve for p_1 and p_2 separately.

We take a derivative of log-likelihood function with respect to p_1, set it equal to zero and solve for p_1. Note that when we differentiate log-likelihood function the terms involving p_2 will have derivative equal to zero. So we only work with data from experiments involving coin 1.

The answer we get makes sense intuitively: it is the total number of heads we got in experiments with coin 1 divided by total number of flips in experiments with coin 1. Calculations for p_2 will be similar.

Now I will implement this solution in Python.

This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters

Show hidden characters

	m = 10 # number of flips in experiment
	n = 5 # number of experiments

	p_1 = 0.8
	p_2 = 0.3

	xs = [] # number of heads in each experiment
	zs = [0,0,1,0,1] # which coin to flip

	np.random.seed(5)
	for i in zs:
	if i==0:
	xs.append(stats.binom(n=m, p=p_1).rvs()) # flip coin 1
	elif i==1:
	xs.append(stats.binom(n=m, p=p_2).rvs()) # flip coin 2

	xs = np.array(xs)
	print(xs)

	exp1 = [0,1,3] # indexes of experiments with coin 1
	exp2 = [2,4] # indexes of experiments with coin 2

	print('Analytical solutions:')
	print('p1: ', xs[exp1].sum() / (m * len(exp1)))
	print('p2: ', xs[exp2].sum() / (m * len(exp2)))

view raw em_coinflip_complete_a.py hosted with ❤ by GitHub

Everything is simple. We just implement the formulas we calculated above and plug in the numbers. The results of running this code are shown below.

Another way to solve this problem is using numerical solvers. Recall that we need to find a solution that maximizes log-likelihood function. When we use numerical solvers we don’t need to calculate derivatives and manually solve for parameters that maximize log-likelihood function. We just implement a function we want to maximize and pass it to numerical solver.

Since most solvers in Python are designed to minimize a given function, we implement a function that calculates negative log-likelihood (because minimizing negative log-likelihood function is the same as maximizing log-likelihood function).

Code and results are shown below.

Show hidden characters

	def neg_log_likelihood(probs, m, xs, zs):
	'''
	compute negative log-likelihood
	'''
	ll = 0
	for x,z in zip(xs,zs):
	ll += stats.binom(p=probs[z], n=m).logpmf(x)

	return -ll

	res = optimize.minimize(neg_log_likelihood, [0.5,0.5], bounds=[(0,1),(0,1)], args=(m,xs,zs), method='tnc')

	print('Numerical solution:')
	print('p1: ', res.x[0])
	print('p2: ', res.x[1])

view raw em_coinflip_complete_n.py hosted with ❤ by GitHub

As you can see we get the same results as in analytical solution.

Now assume that we don’t know which coin was used in each experiment. In that case variable Z is not observed (it is called latent or hidden variable) and the data set becomes incomplete. Estimating probabilities p_1 and p_2becomes harder now, but we can still do it with the help of EM algorithm.

If we know probabilities of selecting coin 1 or coin 2, we can use Bayes’ theorem to estimate the bias of each coin. If we know the bias of each coin, we can estimate probabilities that in a given experiment coin 1 or coin 2 was used. In the EM algorithm we make initial guess about those probabilities and then iterate between two steps (estimating bias given probabilities of using each coin and estimating probabilities of using each coin given bias) until convergence. It can be proved mathematically that such algorithm converges to a local maximum (of likelihood function).

Let’s try to replicate example provided in the paper. The problem setup is shown below.

Complete dataset consists of two variables X and Z, but only X is observed. Since one of two coins is selected at random, the probability of selecting each coin is equal to 0.5. To solve for theta we need to maximize the following likelihood function:

The function above is called incomplete likelihood function. If we compute its logarithm we get:

The summation under logarithm makes maximization problem difficult.

Let’s include hidden variable Z into likelihood function to get complete likelihood:

Then the log of complete likelihood function is:

Here we don’t have a summation inside logarithm and it is easier to solve maximization problem for this function. But, since the values of Z are not observed, we can’t calculate and maximize this function directly. However, if we know the distribution of Z we can calculate its expected value and use it to maximize the likelihood (or log-likelihood) function.

The problem here is that to find the distribution of Z we need to know parameters theta and to find parameters theta we need to know the distribution of Z. EM algorithm allows us to solve this problem. We start with a random guess of parameters theta and then iterate the following steps:

Expectation step (E-step): compute the conditional expectation of the complete log-likelihood function with respect to the current conditional distribution of Z given data X and current parameter estimate theta
Maximization step (M-step): find values of parameters theta that maximize that expectation

We can find the conditional distribution of Z_i given X_i and theta using Bayes’ theorem:

Now we define conditional expectation of the complete log-likelihood as follows:

Plugging in our complete log-likelihood function and rearranging:

This completes E-step. In the M-step we maximize the function calculated above with respect to the parameters theta:

In our example the parameters can be found analytically (by taking a derivative and setting it equal to zero). I will not demonstrate the whole process, just provide the answers.

Now we are ready to implement it. I am going to use the same data as used in the paper to check that we obtain the same results. Python code is provided below.

Show hidden characters

	m = 10 # number of flips in each sample
	n = 5 # number of samples
	xs = np.array([5,9,8,4,7])

	theta = [0.6, 0.5] # initial guess p_1, p_2

	for i in range(10):
	p_1,p_2 = theta
	T_1s = []
	T_2s = []

	# E-step
	for x in xs:
	T_1 = stats.binom(n=m,p=theta[0]).pmf(x) / (stats.binom(n=m,p=theta[0]).pmf(x) +
	stats.binom(n=m,p=theta[1]).pmf(x))
	T_2 = stats.binom(n=m,p=theta[1]).pmf(x) / (stats.binom(n=m,p=theta[0]).pmf(x) +
	stats.binom(n=m,p=theta[1]).pmf(x))

	T_1s.append(T_1)
	T_2s.append(T_2)


	# M-step
	T_1s = np.array(T_1s)
	T_2s = np.array(T_2s)
	p_1 = np.dot(T_1s, xs) / (m * np.sum(T_1s))
	p_2 = np.dot(T_2s, xs) / (m * np.sum(T_2s))
	print(f'step:{i}, p1={p_1:.2f}, p2={p_2:.2f}')
	theta = [p_1, p_2]

view raw em_coinflip_inc.py hosted with ❤ by GitHub

All parameters are exactly the same as in the paper. Below you can see the diagram from the paper and the output of the code above.

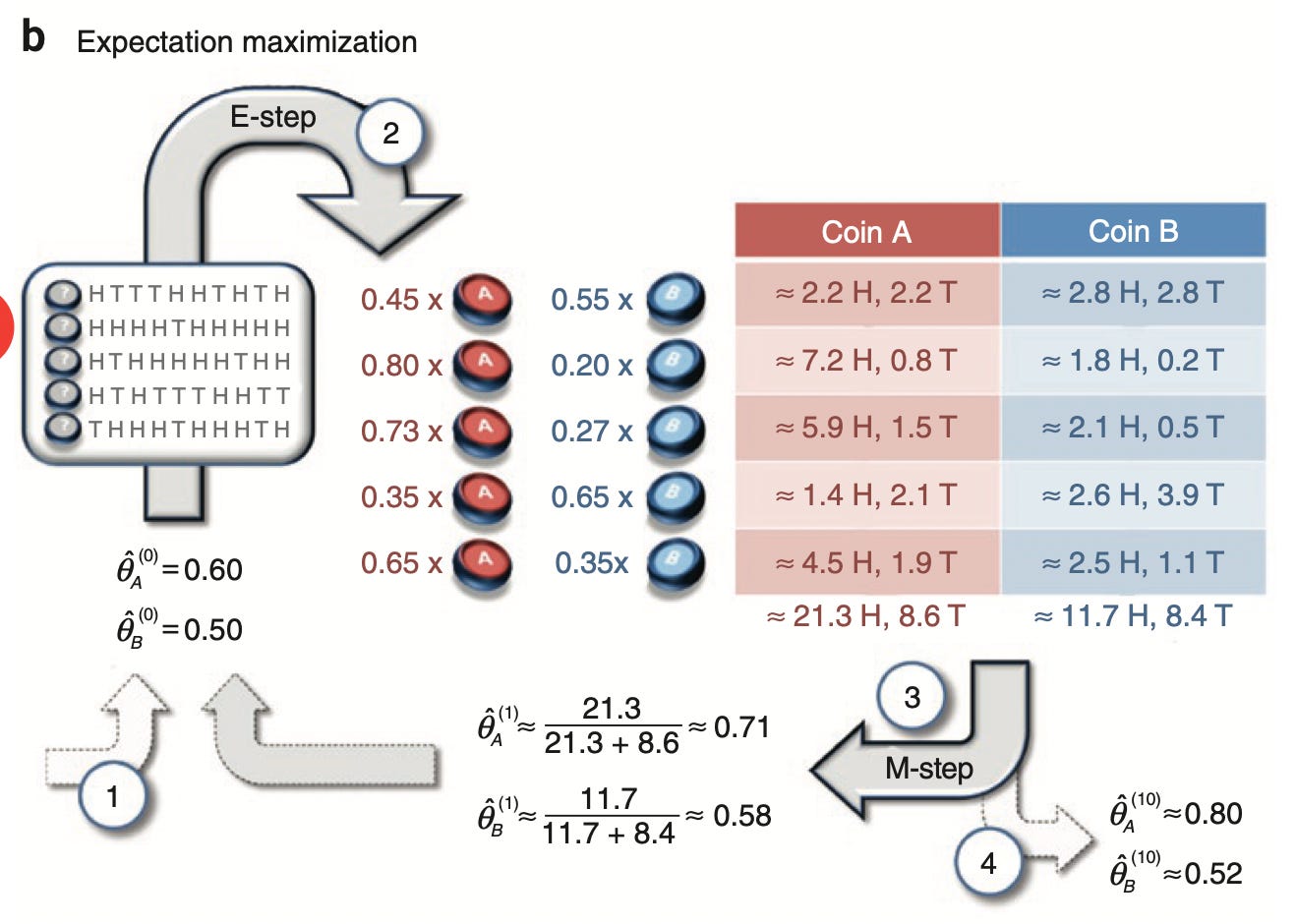
We were able to get exactly the same results as in the paper, which means that the EM-algorithm was implemented correctly.

It is also possible to use numerical solvers for maximizing the conditional expectation of complete log-likelihood function, but I believe in this case it is easier to use analytical solution.

Now let’s try to make the problem a little more complicated. Assume that probabilities of selecting each coin are unknown. Now we have a mixture of two binomials with probability tau of selecting the first coin and probability 1-tau of selecting the second coin.

We repeat the same steps as before. Define complete likelihood function:

In the previous example the conditional probability of Z given theta was constant, now it is a PMF of Bernoulli distribution with parameter tau.

Calculate complete log-likelihood function:

Find conditional distribution of hidden variable Z given X and theta:

Calculate conditional expectation of the log-likelihood:

Conditional expectation of log-likelihood

What’s left is to maximize the conditional expectation with respect to parameters theta. The terms involving probabilities p_j in the formula above are exactly the same as we had before, so solutions for p_1 and p_2 will be the same. Maximizing the conditional expectation with respect to tau we get:

Now we are ready to implement this algorithm in Python. Code for it is shown below.

Show hidden characters

	# model parameters
	p_1 = 0.1
	p_2 = 0.8
	tau_1 = 0.3
	tau_2 = 1-tau_1

	m = 10 # number of flips in each sample
	n = 10 # number of samples

	# generate data
	np.random.seed(123)
	dists = [stats.binom(n=m, p=p_1), stats.binom(n=m, p=p_2)]
	xs = [dists[x].rvs() for x in np.random.choice([0,1], size=n, p=[tau_1,tau_2])]

	# random initial guess
	np.random.seed(123)
	theta = [np.random.rand() for _ in range(3)]

	last_ll = 0
	max_iter = 100

	for i in range(max_iter):
	tau,p_1,p_2 = theta
	T_1s = []
	T_2s = []

	# E-step
	lls = []
	for x in xs:
	denom = (tau * stats.binom(n=m,p=p_1).pmf(x) + (1-tau) * stats.binom(n=m,p=p_2).pmf(x))
	T_1 = tau * stats.binom(n=m,p=p_1).pmf(x) / denom
	T_2 = (1-tau) * stats.binom(n=m,p=p_2).pmf(x) / denom
	T_1s.append(T_1)
	T_2s.append(T_2)
	lls.append(T_1 * np.log(tau * stats.binom(n=m,p=p_1).pmf(x)) +
	T_2 * np.log(tau * stats.binom(n=m,p=p_2).pmf(x)))

	# M-step
	T_1s = np.array(T_1s)
	T_2s = np.array(T_2s)
	tau = np.sum(T_1s) / n
	p_1 = np.dot(T_1s, xs) / (m * np.sum(T_1s))
	p_2 = np.dot(T_2s, xs) / (m * np.sum(T_2s))
	print(f'step:{i}, tau={tau}, p1={p_1:.2f}, p2={p_2:.2f}, log_likelihood={sum(lls):.2f}')
	theta = [tau, p_1, p_2]

	# stop when likelihood doesn't improve anymore
	if abs(sum(lls) - last_ll) < 0.001:
	break
	else:
	last_ll=sum(lls)

view raw em_bin_mixture.py hosted with ❤ by GitHub

In the previous example we ran the algorithm for 10 iterations to replicate the results in the paper. In practice we run the algorithm until convergence, meaning that we stop the algorithm when the log-likelihood stops improving.

Output of the algorithm is shown above. Note that because of the symmetry of the problem probabilities p_1 and p_2 are switched. The results are still correct and close to true values of the parameters: we have p=0.85 with probability 0.8 and p=0.1 with probability 0.2 (true values: p=0.8 with probability 0.7 and p=0.1 with probability 0.3).

The goal of this article was to demonstrate the basics of EM-algorithm on some simple examples. In the next article I will try to implement EM-algorithm for another (more difficult) statistical model and build a pairs trading strategy based on it.

Jupyter notebook with source code is available here.

If you have any questions, suggestions or corrections please post them in the comments. Thanks for reading.

References

[1] What is the expectation maximization algorithm? (Do & Batzoglou, 2008)

[2] Expectation-maximization algorithm, explained

[3] The EM Algorithm

[4] What is an intuitive explanation of the Expectation Maximization technique?

[5] Expectation Maximization with Coin Flips

Financial Noob

Discussion about this post