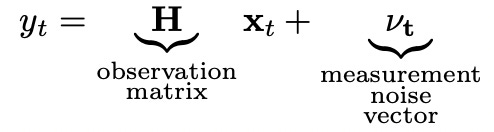Introduction to state-space models and Kalman filters
Understanding the basics of state-space models.
In this post I will describe the main ideas behind state-space models and Kalman filters and try to explain how they work using simple examples. In the following article I will apply these ideas to implementing and backtesting a pairs trading strategy.
State-space models help us analyse time series problems that involve dynamical systems. They are widely used in statistics, econometrics, engineering, computer science and finance. Typically state-space models describe the relationship between some hidden (unknown) variables and their observed measurements. Basically we are trying to get more accurate information about the current state of the system (hidden variables) by using both the measurements and our knowledge about the system (how it evolves in time). For example, in case of GPS systems we measure the time of arrival of signals from the satellites and use it to infer the position and velocity of the system. Position and velocity are hidden variables since they are not directly observed. Apart from that many traditional time series models can be represented in state-space form.
Our goal is to infer the properties of the hidden variable given observed measurements. There are three main types of inference:
Filtering — removing measurement error from the data (trying to estimate the true value of the hidden variable from the observed variables).
Forecasting — predicting the future values of observed or hidden variables.
Smoothing — trying to estimate the past values of hidden variable from the measurements up to some future time.
We will begin with the first two types.
Let’s start with the simplest possible example. Assume that we have a static system that doesn't change over time. So its next state is always equal to its current state. At each time step we make measurements of the current state, but our measuring device is not perfect, so each measurement contains some noise. Such system can be described by the following equations:
State equation describes the development of the hidden variable over time. Measurement equation describes the relationship between the measurement (observed variable) and the state (hidden variable). In the simplest cases our state and measurement variables are just scalar numbers, but in many practical applications they can be vectors (e.g., position and velocity vector in GPS systems).
At each time step we can take our measurement and update our belief about the current state of the system given our knowledge of system dynamics (in this particular case, the fact that the system is static). Assume the we have the following state update equation:
It can be shown that this equation just iteratively calculates the mean of the measurements (see derivation here).
Now let’s try to model such system in Python. The source code for that is provided below.
| n = 25 | |
| np.random.seed(88) | |
| x = np.array([100]*n) # actual states | |
| y = x + np.random.randn(n) # measurements | |
| x_pred = np.zeros(len(x)) # predicted (extrapolated) states | |
| x_filt = np.zeros(len(x)) # estimated (filtered) states | |
| for t in range(len(x)): | |
| if t==0: | |
| x_filt[t] = y[t] # initial guess = first measurement | |
| x_pred[t] = x_filt[t] | |
| else: | |
| x_pred[t] = x_filt[t-1] # extrapolate current state from previous estimate | |
| x_filt[t] = x_pred[t] + 1/(t+1) * (y[t] - x_pred[t]) # estimate current state | |
| plt.figure(figsize=(18,6)) | |
| plt.plot(np.arange(n), x, label='true value', linestyle='dotted') | |
| plt.scatter(np.arange(n), y, label='measurement', marker='x', c='g') | |
| plt.plot(np.arange(n), x_filt, label='estimates', marker='o', linestyle='dashed') | |
| plt.legend() |
First we make a guess about the state of the system (I made it equal to the first measurement). Then at each time step we estimate the new state of the system given the new measurement and our belief (prediction) about what the current state should be according to our knowledge of the system. We know that the system is static, so our prediction is that the next state of the system is the same as the current state. Next we need to incorporate the new measurement into our estimate of the state. We do it according to the state update equation presented above. The evolution of the system is presented on the plot below.
You can see that at each time step we are getting closer and closer to the true value. Below you can see the values of each variable at each time step (for first 12 steps), so that you can check that the variables evolve according to the equations presented earlier.
Now let’s assume the system is dynamic. We know that its growth rate is constant and is equal to 1. Our state and measurement equations change only a little bit:
Our state update equation also changes. Note that before (when our system was static) each measurement contributed less and less to the current state estimate (we had a factor of 1/(t+1) in state update equation). Now, since our system is dynamic, new information plays a big role in the current state estimate. That’s why we change 1/(t+1) to g:
Factor g plays is important here and must be chosen carefully. It determines how much we believe in our measurement versus our model predictions. High values of g will give more weight to measurements and less weight to model predictions and vice versa. In this example I will set g=0.1 indicating that we are pretty confident in the accuracy of our model.
Source code, plots and values of the variable during first several steps are provided below.
| n = 25 | |
| np.random.seed(88) | |
| x = np.arange(100,100+n) # actual states | |
| y = x + np.random.randn(n) # measurements | |
| x_pred = np.zeros(len(x)) # predicted (extrapolated) states | |
| x_filt = np.zeros(len(x)) # estimated (filtered) states | |
| g = 0.1 | |
| growth_rate = 1 | |
| for t in range(len(x)): | |
| if t==0: | |
| x_filt[t] = y[t] # initial guess = first measurement | |
| x_pred[t] = x_filt[t] | |
| else: | |
| x_pred[t] = x_filt[t-1] + growth_rate # extrapolate current state from previous estimate | |
| x_filt[t] = x_pred[t] + g*(y[t] - x_pred[t]) # estimate current state | |
| plt.figure(figsize=(18,6)) | |
| plt.plot(np.arange(n), x, label='true value', linestyle='dotted') | |
| plt.scatter(np.arange(n), y, label='measurement', marker='x', c='g') | |
| plt.scatter(np.arange(n), x_pred, label='predictions', marker='s', c='grey') | |
| plt.plot(np.arange(n), x_filt, label='estimates', marker='o', linestyle='dashed') | |
| plt.legend() |
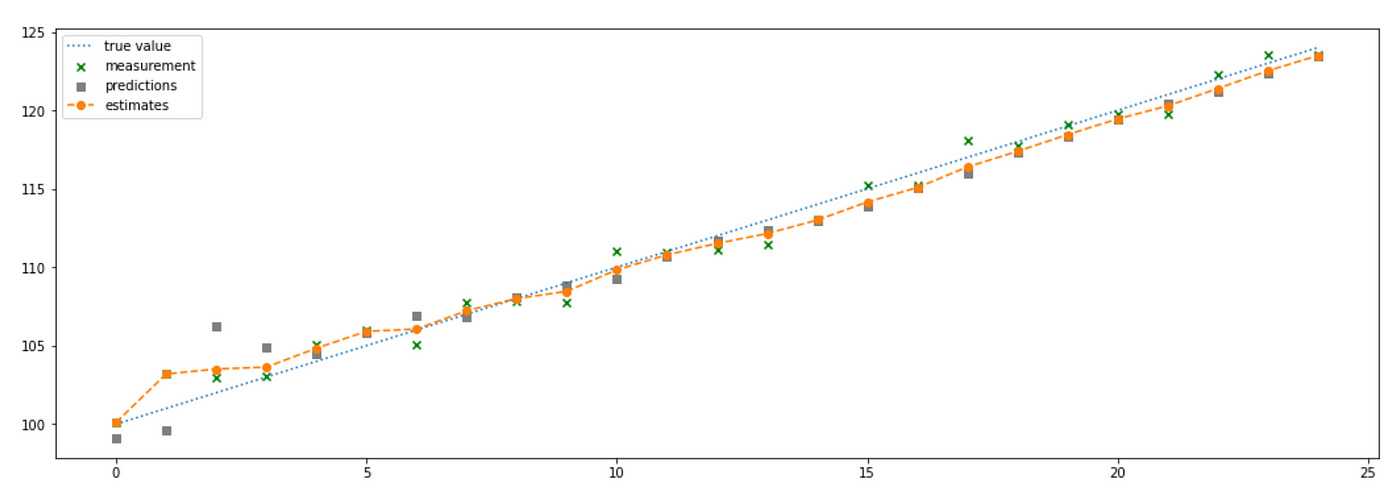
As you can see the estimates provided by our filter almost exactly match the true value of the state. But what if our assumption about the growth rate was wrong? Let’s see what happens. Below is the plot of the similar system with growth rate set to -1.
One of the assumptions of our model is wrong, but low value of g indicates that we give more weight to the model predictions instead of measurements. This leads to bad results depicted on the plot above. Let’s see what happens if we set g=0.5 giving equal weights to measurements and model predictions.
Our estimates are significantly improved, but they are still far from true values. The reason for this is that we made very strong assumptions about the system dynamics which turned out to be false.
Let’s try to fix the problem encountered in the last example. We will assume that the growth rate is still constant, but it is not known to us. State and measurement equations for such system will be:
Note that now we have two state variables (x, and its growth rate) and two state equations describing their evolution. Why don’t we also have two measurement equations? Because we don’t directly measure the growth rate. We only measure the value of x at each time step and from those measurements we can try to infer the growth rate. Also since now we have two state variables, we also have two state update equations:
Note that now state update equations require two parameters— g and h — one for each equation. In the example below I set them both equal to 0.5. I also specifically set the initial growth rate equal to -1 to test how this system behaves if we make wrong assumptions.
| n = 25 | |
| np.random.seed(88) | |
| x = np.arange(100,100+n) # actual states | |
| y = x + np.random.randn(n) # measurements | |
| dx = np.zeros(len(x)) # estimated growth rates | |
| x_pred = np.zeros(len(x)) # predicted (extrapolated) states | |
| x_filt = np.zeros(len(x)) # estimated (filtered) states | |
| g = 0.5 | |
| h = 0.5 | |
| for t in range(len(x)): | |
| if t==0: | |
| x_filt[t] = y[t] # initial guess = first measurement | |
| dx[t] = -1 # initial guess of growth rate | |
| x_pred[t] = x_filt[t] | |
| else: | |
| x_pred[t] = x_filt[t-1] + dx[t-1] # extrapolate current state | |
| dx[t] = dx[t-1] + h*(y[t] - x_pred[t]) # estimate growth rate | |
| x_filt[t] = x_pred[t] + g*(y[t] - x_pred[t]) # estimate current state | |
| plt.figure(figsize=(18,6)) | |
| plt.plot(np.arange(n), x, label='true value', linestyle='dotted') | |
| plt.scatter(np.arange(n), y, label='measurement', marker='x', c='g') | |
| plt.scatter(np.arange(n), x_pred, label='predictions', marker='s', c='grey') | |
| plt.plot(np.arange(n), x_filt, label='estimates', marker='o', linestyle='dashed') | |
| plt.legend() |
As you can see on the plot and in the table above our filter gives quite accurate estimates of the true state. Even though we made a wrong assumption about the growth rate, it was quickly corrected.
Note that the results obtained depend on the choice of parameters g and h. Poor choice of parameters will lead to poor results as demonstrated on the plot below. Another limitation is that parameters g, h are constant.
Anyway such filter (called g-h filter or alpha-beta filter) is a huge improvement compared to using just noisy measurements. It allows us to make more or less accurate estimates of the state even when we don’t have very good model of the system and\or very accurate measurements.
Now we are ready to talk about Kalman filters. Basically Kalman filters are very similar to the g-h filter presented above, just a little more complicated. I’m going to start with simple static system again. Before we begin I need to introduce some additional notation.
Measurement uncertainty is just variance of the measurement error. Estimate uncertainty is variance of our estimate. It is updated at each step. Process noise variance indicates our belief in the accuracy of the model we use. Kalman gain plays the same role as parameters g and h, but unlike them it is updated at each time step. Everything else we already know.
Key difference from the g-h filter: in addition to the state variable we now have state covariance variable (estimate uncertainty) and Kalman gain variable, which are updated at each time step.
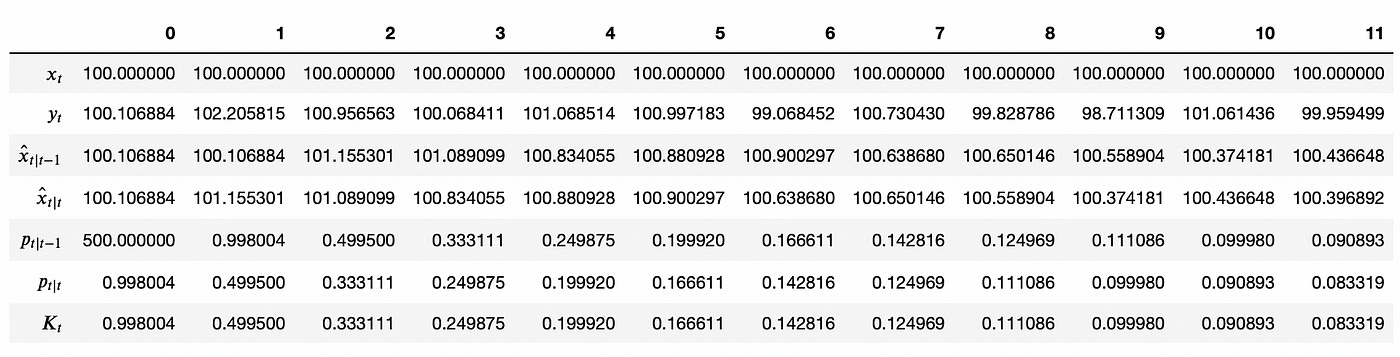
You can look at the algorithm in the code below. The code is commented and I believe everything should be very clear. It is basically the same g-h filter but with a couple of additional steps.
| n = 25 | |
| np.random.seed(88) | |
| x = np.array([100]*n) # actual states | |
| r = 1 # measurement variance | |
| y = x + np.random.randn(n)*np.sqrt(r) # measurements | |
| p_pred = np.zeros(len(x)) # predicted (extrapolated) estimate variance | |
| p = np.zeros(len(x)) # estimated (filtered) estimate variance | |
| q = 0 # process noise variance | |
| K = np.zeros(len(x)) # Kalman gain | |
| x_pred = np.zeros(len(x)) # predicted (extrapolated) states | |
| x_filt = np.zeros(len(x)) # estimated (filtered) states | |
| # initial guess of state and estimate uncertainty | |
| x_0 = y[0] | |
| p_0 = 500 | |
| for t in range(len(x)): | |
| if t==0: | |
| x_pred[t] = x_0 # initial guess = first measurement | |
| p_pred[t] = p_0 # inital guess | |
| K[t] = p_pred[t] / (p_pred[t] + r) | |
| p[t] = (1 - K[t]) * p_pred[t] | |
| x_filt[t] = x_pred[t] + K[t]*(y[t] - x_pred[t]) | |
| else: | |
| x_pred[t] = x_filt[t-1] # state extrapolation | |
| p_pred[t] = p[t-1] + q # covariance extrapolation | |
| K[t] = p_pred[t] / (p_pred[t] + r) # Kalman gain | |
| x_filt[t] = x_pred[t] + K[t]*(y[t] - x_pred[t]) # state estimation | |
| p[t] = (1 - K[t]) * p_pred[t] # covariance estimation | |
| plt.figure(figsize=(18,6)) | |
| plt.plot(np.arange(n), x, label='true value', linestyle='dotted') | |
| plt.scatter(np.arange(n), y, label='measurement', marker='x', c='g') | |
| plt.scatter(np.arange(n), x_pred, label='predictions', marker='s', c='grey') | |
| plt.plot(np.arange(n), x_filt, label='estimates', marker='o', linestyle='dashed') | |
| plt.legend() |
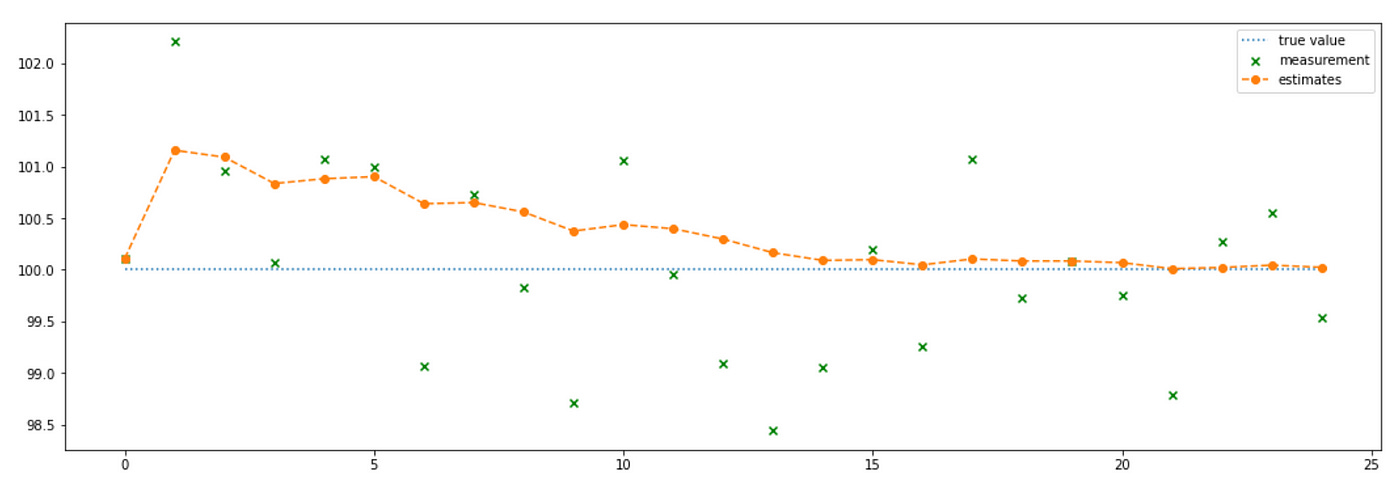
Here again we basically iteratively calculate the mean of the measurements. Note how Kalman gain gradually decreases giving less and less weight to the new measurements. Also note that even though I set initial estimate uncertainty very high, it decreases very quickly in the next time step and continues to decrease gradually over the following steps.
Now let’s apply Kalman filter to a dynamic system (also one-dimensional for now). The code here is exactly the same as before, we just need to set the process noise to some positive value to indicate the fact the the state might change, but without making any assumptions about the growth rate.
We can see that even without any assumptions about the dynamics of the system, Kalman filter is able to adjust and give us somewhat acceptable estimates. You can note that in most time steps our estimates are lower than the true value of the state. This happens because the parameter q (process noise) is set to a low value indicating that we put a lot of weight in our model predictions. But our model assumes that the state is static (does not change), which is not the case.
Now I will introduce multidimensional Kalman filter. It will help us solve the problem encountered above. Recall that when we modeled dynamic system with linear growth we introduced another state variable for a growth rate. We will do the same thing here, but instead of introducing another variable, we will make our state variable a 2-dimensional vector. The algorithm basically remains the same, but now we are dealing with vectors and matrices instead of scalar numbers.
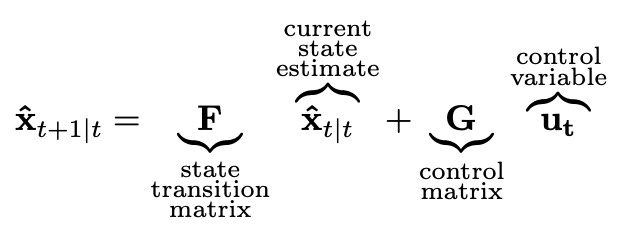
Let me try to explain what exactly changes using the same example — system with constant growth rate. Let’s begin with the state equation. In multiple dimensions it looks like this (bold lowercase letters represent vectors and bold uppercase letters represent matrices):
Control matrix and control variable are used when we have some input to the system. We don’t use them in our simple example. But we do use the state transition matrix F and we need to design it according to our model. Recall how we defined our model in one dimension.
Note that we can rewrite these equations in matrix form:
So now our state is represented by two-dimensional vector and to calculate the next state from the current state we multiply current state vector by state transition matrix F. Now let’s look at the measurement equation.
In our simple example the measurements are scalar because we only measure one variable. Observation matrix H should be designed accordingly.
Measurement noise is also scalar in this case.
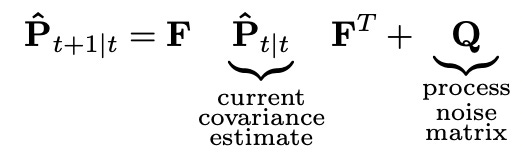
Now let’s look at the covariance extrapolation equation.
In one-dimensional case we had a scalar estimate variance. Now it is represented by the estimate covariance matrix. Same thing with process noise. (Actually designing a process noise matrix can be a little tricky, but it is out of scope of this article, I will provide some links to resources describing it in more detail).
We will also need a matrix for Kalman gain, which is updated at every time step, and that’s it. We have all building blocks to introduce the rest of Kalman filter equations.
Matrix R in the equations above represents measurement uncertainty matrix. In our example measurements are one-dimensional, so it will be just a scalar number. Now we are ready to implement it. Source code and plots of the simulation are provided below.
| n = 25 | |
| np.random.seed(88) | |
| X = np.vstack([[np.arange(100,100+n)],[np.array([1]*n)]]) # actual states | |
| R = np.array([[1]]) # measurement covariance matrix | |
| Y = X[0,:] + np.random.randn(n)*np.sqrt(R[0,0]) | |
| P_pred = np.zeros((n,X.shape[0],X.shape[0])) | |
| P = np.zeros((n,X.shape[0],X.shape[0])) | |
| K = np.zeros((n,2,1)) | |
| X_pred = np.zeros(X.shape) | |
| X_filt = np.zeros(X.shape) | |
| H = np.array([[1,0]]) # observation matrix | |
| F = np.array([[1,1],[0,1]]) # state transition matrix | |
| Q = np.array([[0,0],[0,0]]) # process noise matrix (for simplicity I assume that our model is perfect) | |
| # initial guess of state and estimate uncertainty | |
| X_0 = np.hstack([Y[0],[-1]]) | |
| P_0 = np.array([[500,0],[0,500]]) | |
| for t in range(X.shape[1]): | |
| if t==0: | |
| X_pred[:,t] = F @ X_0 # state extrapolation | |
| P_pred[t,:] = F @ P_0 @ F.T + Q # covariance extrapolation | |
| K[t,:] = P_pred[t,:] @ H.T @ np.linalg.inv(H @ P_pred[t,:] @ H.T + R) # calculate Kalman gain | |
| X_filt[:,t] = X_pred[:,t] + K[t,:] @ (Y[t] - H @ X_pred[:,t]) # update estimate | |
| P[t,:] = ((np.eye(2) - K[t,:] @ H) @ P_pred[t,:] @ | |
| (np.eye(2) - K[t,:] @ H).T + K[t,:] @ R @ K[t,:].T) # update estimate uncertainty | |
| else: | |
| X_pred[:,t] = F @ X_filt[:,t-1] # state extrapolation | |
| P_pred[t,:] = F @ P[t-1,:] @ F.T + Q # covariance extrapolation | |
| K[t,:] = P_pred[t,:] @ H.T @ np.linalg.inv(H @ P_pred[t,:] @ H.T + R) # calculate Kalman gain | |
| X_filt[:,t] = X_pred[:,t] + K[t,:] @ (Y[t] - H @ X_pred[:,t]) # update state estimate | |
| P[t,:] = ((np.eye(2) - K[t,:] @ H) @ P_pred[t,:] @ | |
| (np.eye(2) - K[t,:] @ H).T + K[t,:] @ R @ K[t,:].T) # update estimate uncertainty | |
| plt.figure(figsize=(18,6)) | |
| plt.plot(np.arange(n), X[0,:], label='true value', linestyle='dotted') | |
| plt.scatter(np.arange(n), Y, label='measurement', marker='x', c='g') | |
| plt.scatter(np.arange(n), X_pred[0,:], label='predictions', marker='s', c='grey') | |
| plt.plot(np.arange(n), X_filt[0,:], label='estimates', marker='o', linestyle='dashed') | |
| plt.legend() |
As you can see the results we get are quite good. Estimates of both elements of the state variable are very close to the true values. Note that this filter can be easily adapted to a lot more difficult problems with more complex models and more dimensions. All equations will be the same. We will just need to design matrices F, H, Q and R according to our model.
Of course we didn’t need to implement everything from scratch, but I believe it was useful for educational purposes. Now I’ll demonstrate how it can be done in Python with FilterPy library. The code is presented below and you can easily check that the results we get with the library exactly match our previous results.
| from filterpy.kalman import KalmanFilter | |
| f = KalmanFilter(dim_x=2, dim_z=1) | |
| f.x = X_0 | |
| f.F = F | |
| f.H = H | |
| f.P = P_0 | |
| f.R = R | |
| f.Q = Q | |
| for y in Y: | |
| f.predict() | |
| f.update(y) | |
| print(f.x) |
One more thing I want to demonstrate is smoothing. Smoothing is basically applying a filter to all available data at once (instead of iteratively to one data point at a time). This allows us to make more accurate estimation of the true state of the system. Let me show you how to implement it with FilterPy and apply it to our example.
| np.random.seed(88) | |
| X = np.vstack([[np.arange(100,100+n)],[np.array([1]*n)]]) # actual states | |
| R = np.array([[1]]) # measurement covariance matrix | |
| Y = X[0,:] + np.random.randn(n)*np.sqrt(R[0,0]) | |
| P_pred = np.zeros((n,X.shape[0],X.shape[0])) | |
| P = np.zeros((n,X.shape[0],X.shape[0])) | |
| K = np.zeros((n,2,1)) | |
| X_pred = np.zeros(X.shape) | |
| X_filt = np.zeros(X.shape) | |
| H = np.array([[1,0]]) # observation matrix | |
| F = np.array([[1,1],[0,1]]) # state transition matrix | |
| Q = np.array([[0,0],[0,0]]) # process noise matrix (for simplicity I assume that our model is perfect) | |
| # initial guess of state and estimate uncertainty | |
| X_0 = np.hstack([Y[0],[-1]]) | |
| P_0 = np.array([[500,0],[0,500]]) | |
| f = KalmanFilter(dim_x=2, dim_z=1) | |
| f.x = X_0 | |
| f.F = F | |
| f.H = H | |
| f.P = P_0 | |
| f.R = R | |
| f.Q = Q | |
| mu,cov,_,_ = f.batch_filter(Y) # filtering | |
| M, P, C, _ = f.rts_smoother(mu, cov) # smoothing | |
| plt.figure(figsize=(18,6)) | |
| plt.plot(np.arange(n), X[0,:], label='true value', linestyle='dotted') | |
| plt.scatter(np.arange(n), Y, label='measurement', marker='x', c='g') | |
| plt.plot(np.arange(n), mu[:,0], label='filter', marker='o', linestyle='dashed') | |
| plt.plot(np.arange(n), M[:,0], label='smoother', marker='.', c='m') | |
| plt.legend() |
You can see above that smoother provides us with estimates which almost exactly match the true states. Now I will show how it can be applied to real data.
For this example I will use realized 10min volatility of Alcoa stock from Jan 2, 2003 to May 7, 2004. The same data was used in Ruey S. Tsay book ‘Analysis of Financial Time Series’. It can be downloaded here. Code for Kalman filtering and smoothing is provided below.
| R = np.array([[10]]) # measurement covariance matrix | |
| Y = np.log(np.genfromtxt('aa-3rv.txt')[:,1]) # log of realized volatility | |
| H = np.array([[1,0]]) # observartion matrix | |
| F = np.array([[1,1],[0,1]]) # state transition matrix | |
| Q = np.array([[1,0],[0,1]]) # process noise matrix | |
| # initial guess of state and estimate uncertainty | |
| X_0 = np.hstack([[0],[0]]) | |
| P_0 = np.array([[1000,0],[0,1000]]) | |
| f = KalmanFilter(dim_x=2, dim_z=1) | |
| f.x = X_0 | |
| f.F = F | |
| f.H = H | |
| f.P = P_0 | |
| f.R = R | |
| f.Q = Q | |
| mu,cov,_,_ = f.batch_filter(Y) # filtering | |
| M, P, C, _ = f.rts_smoother(mu, cov) # smoothing | |
| plt.figure(figsize=(18,6)) | |
| plt.plot(np.arange(len(Y)), Y, label='measurement', marker='x', c='g', linestyle='dotted') | |
| plt.plot(np.arange(len(Y)), mu[:,0], label='filter', marker='o', linestyle='dashed') | |
| plt.plot(np.arange(len(Y)), M[:,0], label='smoother', marker='.', c='m') | |
| plt.legend() |
Now I will show a portion of the plot above to better see the difference between filtered and smoothed estimates.
As expected the estimates provided by the smoother are less erratic and less variable than the estimates provided by the filter.
I hope that now you have a better understanding of state space models and Kalman filters. If some parts are still unclear or if you want more detailed explanations please check the references below. I believe that having at least some knowledge of the basic building blocks behind these ideas can be very useful when we try to apply state space models in practice. In the next post I will use that knowledge to implement and backtest a pairs trading strategy described in this paper.
Jupyter notebook with source code is available here.
If you have any questions, suggestions or corrections please post them in the comments. Thanks for reading.
References
[1] https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python