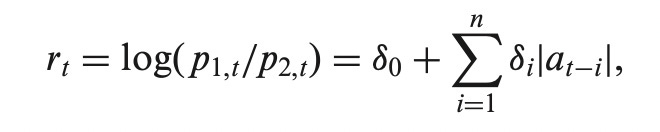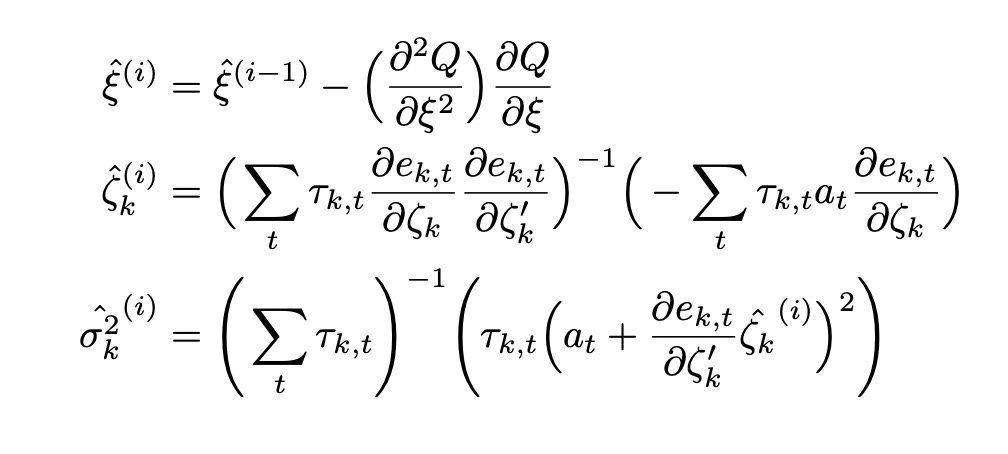Expectation Maximization for Logistic Mixture Autoregressive (LMAR) model
Applying EM algorithm to regime-switching autoregressive processes.
In this article I will describe my unsuccessful attempt to replicate simulation studies from the paper ‘Basket trading under co-integration with the logistic mixture autoregressive mode’ (Cheng et al. 2011). It describes statistical arbitrage strategy where the spread is assumed to follow logistic mixture autoregressive (LMAR) model. My initial idea was to implement and backtest such strategy, but for some reason my implementation of the Expectation Maximization algorithm does not perform as well as described in the paper. Maybe trying to describe my process here will help me find a solution, or maybe someone from the audience will spot my mistake and let me know.
(Please note that the problem was solved and solution was published in another article)
Basically the proposed LMAR model suggests that at a given time t the realization of the spread comes from one of two processes (regimes) with probability of being in each regime determined by the logistic equation shown below.
The mixing probabilities are dynamic and depend of previous realizations of the process. Given information up to time t-1, the CDF of the spread a at timet is defined as follows:
Basically what it says is that realization of a_t comes from a normal distribution with mean e_1,t and standard deviation sigma_1 with probability p_1,t and from normal distribution with mean e_2,t and standard deviation sigma_2 with probability p_2,t. In the first equation above Phi is the CDF of standard normal distribution.
The means e_1 and e_2 are dynamic and follow AR processes. Standard deviations are fixed. The code for generating a sample from LMAR process is shown below.
| def generate_a(N, ksi, zeta_1, var_1, zeta_2, var_2): | |
| ''' | |
| generate a of size N with given parameters | |
| ''' | |
| a = np.zeros(N) | |
| p1 = np.zeros(N) | |
| p2 = np.zeros(N) | |
| for i in range(N): | |
| # find lags of a_t | |
| if i>=2: | |
| a_lag1 = a[i-1] | |
| a_lag2 = a[i-2] | |
| elif i==1: | |
| a_lag1 = a[i-1] | |
| a_lag2 = 0 | |
| elif i==0: | |
| a_lag1 = 0 | |
| a_lag2 = 0 | |
| # solve probability equation | |
| p1[i] = (np.exp(np.dot(ksi, [1, abs(a_lag1), abs(a_lag2)])) / | |
| (1 + np.exp(np.dot(ksi, [1, abs(a_lag1), abs(a_lag2)])))) | |
| p2[i] = 1-p1[i] | |
| # calculate means of two regimes | |
| e1 = np.dot(zeta_1, np.array([1, a_lag1, a_lag2])) | |
| e2 = np.dot(zeta_2, np.array([1, a_lag1])) | |
| regime = np.random.choice([1,2], p=[p1[i],p2[i]]) | |
| if regime==1: | |
| a[i] = stats.norm(loc=e1, scale=np.sqrt(var_1)).rvs() | |
| else: | |
| a[i] = stats.norm(loc=e2, scale=np.sqrt(var_2)).rvs() | |
| return a |
The probability equation is solved analytically as follows:
After solving for mixing probabilities we calculate the means e1 and e2 and we are ready to generate a_t. First we choose the current regime according to the mixing probabilities and then generate a random variable from the distribution corresponding to the selected regime. In the paper there is a theorem with a proof that the spread generated from such model is stationary (when some conditions on logistic equation are satisfied).
Before we continue let me introduce some notation we are going to need.
Below you can see the code for generating and plotting the spread with parameters used in simulation studies in the paper.
| N = 500 # number of datapoints to generate | |
| ksi = [-1.3, 0.6, 0.3] | |
| zeta_1 = [0, 0.6, -0.2] | |
| var_1 = 1 | |
| zeta_2 = [0, 1.5] | |
| var_2 = 3 | |
| np.random.seed(5) | |
| a = generate_a(N, ksi, zeta_1, var_1, zeta_2, var_2) | |
| plt.figure(figsize=(18,6)) | |
| plt.plot(a) |
In the paper authors proceed with generating a response variable as a linear combination of several random vectors and generated spread a. OLS is then applied to those vectors to calculate residuals. Then EM algorithm is run on residuals to estimate parameters of the LMAR model. I will skip this step for now since it introduces additional level of complexity and just try to implement EM algorithm and apply it directly to the generated spread a.
All of the formulas for implementing EM algorithm are provided in the paper. If you are not familiar with the basics of the EM algorithm you can read my previous article — ‘Introduction to Expectation Maximization algorithm’.
The formula for the log-likelihood for the complete dataset is shown below.
The variable Z above is an indicator of the current regime. When we are in regime 1 Z_1,t=1 and Z_2,t=0 and vice versa. These variables are not known, but we can replace them with their expected values. Formula for that is provided below.
That’s all we need to know to implement the E-step. Given current values of the parameters we solve the probability equation, calculate e1 and e2 and plug them into the formula above to calculate tau_1 and tau_2.
During M-step we maximize the expected value of log-likelihood with respect to each of the parameters. Again, all of the required formulas are provided in the paper. Function Q below is the expected value of log-likelihood function (it’s the same formula for log-likelihood with taus instead of Zs).
In the formula for calculating variance in the paper the last term was not squared. I believe that it’s a typo. According to another paper on LMAR model (On a logistic mixture autoregressive model (Wong and Li, 2001)) the last term must be squared. It allows us to be sure that the end result is positive. Otherwise we can get a negative results, which can’t be correct since variance must be nonnegative.
Several other formulas we will need:
Now we have everything we need to know to implement EM algorithm. My implementation of the EM-algorithm is provided below.
| def outer(x): | |
| ''' | |
| calculate outer product of a vector x with itself | |
| ''' | |
| return np.outer(x,x) | |
| def em_algorithm(a, max_iter, tol): | |
| ''' | |
| run em algorithm for max_iter iterations or until convergence | |
| ''' | |
| npdf = stats.norm.pdf | |
| converged = False | |
| while not converged: | |
| try: | |
| # random initial guess | |
| ksi = np.random.uniform(-3,3,(3)) | |
| zeta_1 = np.random.uniform(-3,3,(3)) | |
| zeta_2 = np.random.uniform(-3,3,(2)) | |
| var_1 = np.random.uniform(0,6,(1)) | |
| var_2 = np.random.uniform(0,6,(1)) | |
| # true values | |
| #ksi = np.array([-1.3,0.6,0.3]) | |
| #zeta_1 = np.array([0,0.6,-0.2]) | |
| #zeta_2 = np.array([0,1.5]) | |
| #var_1 = np.array([1]) | |
| #var_2 = np.array([3]) | |
| # create dataframe | |
| df = pd.DataFrame(columns=['const', 'a', 'a_l1', 'a_l2', 'abs_l1', 'abs_l2', 'p1', 'p2', | |
| 'tau1', 'tau2', 'e1', 'e2']) | |
| df['a'] = a[2:] | |
| df['a_l1'] = a[1:-1] | |
| df['a_l2'] = a[:-2] | |
| df['abs_l1'] = abs(df['a_l1']) | |
| df['abs_l2'] = abs(df['a_l2']) | |
| df['const'] = 1 | |
| for s in range(max_iter): | |
| # E-step | |
| # solve for mixing probabilities | |
| num = np.exp((df[['const', 'abs_l1', 'abs_l2']] * ksi).sum(axis=1)) | |
| denom = (1 + np.exp((df[['const', 'abs_l1', 'abs_l2']] * ksi).sum(axis=1))) | |
| df['p1'] = num/denom | |
| df['p2'] = 1 - df['p1'] | |
| # calculate e | |
| df['e1'] = df['a'] - (zeta_1 * df[['const', 'a_l1', 'a_l2']]).sum(axis=1) | |
| df['e2'] = df['a'] - (zeta_2 * df[['const', 'a_l1']]).sum(axis=1) | |
| # calculate tau | |
| sigma_1 = np.sqrt(var_1) | |
| sigma_2 = np.sqrt(var_2) | |
| denom = ((df['p1'] / sigma_1) * stats.norm.pdf(df['e1'] / sigma_1) + | |
| (df['p2'] / sigma_2) * stats.norm.pdf(df['e2'] / sigma_2)) | |
| df['tau1'] = (df['p1'] / sigma_1) * stats.norm.pdf(df['e1'] / sigma_1) / denom | |
| df['tau2'] = (df['p2'] / sigma_2) * stats.norm.pdf(df['e2'] / sigma_2) / denom | |
| # M-step | |
| # compute ksi | |
| dr_dksi = df[['const', 'abs_l1', 'abs_l2']] | |
| dQ_dksi = (np.tile((df['tau1'] - df['p1']), (3,1)).T * dr_dksi).sum().values | |
| df['dr_dksi^2'] = df[['const', 'abs_l1', 'abs_l2']].apply(outer, axis=1).apply(np.array) | |
| d2Q_dksi2 = -(df['p1'] * df['p2'] * df['dr_dksi^2']).sum() | |
| new_ksi = ksi - np.linalg.inv(d2Q_dksi2) @ dQ_dksi | |
| # compute zeta | |
| df['de1_dzeta1^2'] = df[['const', 'a_l1', 'a_l2']].apply(outer, axis=1).apply(np.array) | |
| df['de2_dzeta2^2'] = df[['const', 'a_l1']].apply(outer, axis=1).apply(np.array) | |
| zeta1_sum1 = (df['tau1'] * df['de1_dzeta1^2']).sum() | |
| zeta2_sum1 = (df['tau2'] * df['de2_dzeta2^2']).sum() | |
| zeta1_sum2 = (-np.tile(df['tau1'] * df['a'], (3,1)).T * -df[['const', 'a_l1', 'a_l2']]).sum().values | |
| zeta2_sum2 = (-np.tile(df['tau2'] * df['a'], (2,1)).T * -df[['const', 'a_l1']]).sum().values | |
| new_zeta_1 = np.linalg.inv(zeta1_sum1) @ zeta1_sum2 | |
| new_zeta_2 = np.linalg.inv(zeta2_sum1) @ zeta2_sum2 | |
| # compute variance | |
| sigma1_sum2 = (df['tau1'] * (df['a'] + np.dot(-df[['const', 'a_l1', 'a_l2']], new_zeta_1))**2).sum() | |
| sigma2_sum2 = (df['tau2'] * (df['a'] + np.dot(-df[['const', 'a_l1']], new_zeta_2))**2).sum() | |
| new_var_1 = 1/df['tau1'].sum() * sigma1_sum2 | |
| new_var_2 = 1/df['tau2'].sum() * sigma2_sum2 | |
| # calculate the difference between old and new values of parameters | |
| delta_ksi = np.sum(abs(new_ksi - ksi)) | |
| delta_zeta_1 = np.sum(abs(new_zeta_1 - zeta_1)) | |
| delta_zeta_2 = np.sum(abs(new_zeta_2 - zeta_2)) | |
| delta_var_1 = np.sum(abs(new_var_1 - var_1)) | |
| delta_var_2 = np.sum(abs(new_var_2 - var_2)) | |
| # update parameters | |
| ksi = new_ksi | |
| zeta_1 = new_zeta_1 | |
| zeta_2 = new_zeta_2 | |
| var_1 = new_var_1 | |
| var_2 = new_var_2 | |
| # calculate total difference between old and new parameters | |
| delta_total = delta_ksi + delta_zeta_1 + delta_zeta_2 + delta_var_1 + delta_var_2 | |
| # check convergence | |
| if delta_total < tol: | |
| print('Converged at iteration ', s) | |
| converged = True | |
| break | |
| # if any parameter is nan, stop | |
| nansum = (np.isnan(ksi).sum() + np.isnan(zeta_1).sum() + np.isnan(zeta_2).sum() + | |
| np.isnan(var_1).sum() + np.isnan(var_2).sum()) | |
| if nansum != 0: | |
| break | |
| if not converged: | |
| print(f'Algorithm not converged') | |
| print('Repeating with different initital values') | |
| except: | |
| continue | |
| # calculate Q | |
| Q_sum1 = (df['tau1'] * (np.log(df['p1']) - 1/2*np.log(var_1) - df['e1']**2 / (2 * var_1))).sum() | |
| Q_sum2 = (df['tau2'] * (np.log(df['p2']) - 1/2*np.log(var_2) - df['e2']**2 / (2 * var_2))).sum() | |
| Q = Q_sum1 + Q_sum2 | |
| return ksi, zeta_1, var_1, zeta_2, var_2, Q |
Everything is pretty straightforward. We start with random initial guess and then just use the formulas from the paper to calculate parameter updates at each iteration. The algorithm is stopped as soon as updates become small enough or maximum number of iterations is reached. Calculations are done in pandas dataframe for improved performance.
Now let’s try to replicate the simulation studies from the paper. To do this we need to generate 300 different sample paths (a) with N=500 datapoints in each path. We run EM algorithm on each of the samples and save the results.
| delta_0s = [] | |
| delta_1s = [] | |
| delta_2s = [] | |
| phi_10s = [] | |
| phi_11s = [] | |
| phi_12s = [] | |
| phi_20s = [] | |
| phi_21s = [] | |
| var_1s = [] | |
| var_2s = [] | |
| Qs = [] | |
| max_iter=200 | |
| tol = 0.1 | |
| N = 500 # number of datapoints to generate | |
| N_sim = 100 # number of simulations to run | |
| # parameters used to generate a | |
| ksi = [-1.3, 0.6, 0.3] | |
| zeta_1 = [0, 0.6, -0.2] | |
| var_1 = 1 | |
| zeta_2 = [0, 1.5] | |
| var_2 = 3 | |
| for s in range(N_sim): | |
| print() | |
| print('Running sim ', s) | |
| # generate a | |
| np.random.seed(123+s) | |
| a = generate_a(N, ksi, zeta_1, var_1, zeta_2, var_2) | |
| # run EM algorithm | |
| ksi_hat, zeta_1_hat, var_1_hat, zeta_2_hat, var_2_hat, Q = em_algorithm(a, max_iter, tol) | |
| # save results | |
| delta_0s.append(ksi_hat[0]) | |
| delta_1s.append(ksi_hat[1]) | |
| delta_2s.append(ksi_hat[2]) | |
| phi_10s.append(zeta_1_hat[0]) | |
| phi_11s.append(zeta_1_hat[1]) | |
| phi_12s.append(zeta_1_hat[2]) | |
| phi_20s.append(zeta_2_hat[0]) | |
| phi_21s.append(zeta_2_hat[1]) | |
| var_1s.append(var_1_hat) | |
| var_2s.append(var_2_hat) | |
| Qs.append(Q) |
Then I create a dataframe with true value of each parameter and the mean and standard deviation of estimated values of each parameter. Code for it is shown below. Note that I’m removing outliers before calculating mean and standard deviation. I found that this allows to improve the accuracy of estimates.
| # https://www.askpython.com/python/examples/detection-removal-outliers-in-python | |
| def remove_outliers(data): | |
| data = np.array(data) | |
| # don't do anything if there is no variability in data | |
| if data.std() < 0.001: | |
| return data | |
| p75, p25 = np.percentile(data, [75,25]) | |
| iqr = p75-p25 | |
| max_val = p75 + 1.5*iqr | |
| min_val = p25 - 1.5*iqr | |
| data[data>max_val] = np.nan | |
| data[data<min_val] = np.nan | |
| return data | |
| index = [r'$\sigma_1^2$', r'$\phi_{1,0}$', r'$\phi_{1,1}$', | |
| r'$\phi_{1,2}$', r'$\sigma_2^2$', r'$\phi_{2,0}$', r'$\phi_{2,1}$', r'$\delta_0$', r'$\delta_1$', | |
| r'$\delta_2$'] | |
| columns = ['True value', 'Mean of estimates', 'SD of estimates'] | |
| results_df = pd.DataFrame(index=index, columns=columns) | |
| results_df['True value'] = [1, 0, 0.6, -0.2, 3, 0, 1.5, -1.3, 0.6, 0.3] | |
| parameters = [var_1s, phi_10s, phi_11s, phi_12s, var_2s, phi_20s, phi_21s, | |
| delta_0s, delta_1s, delta_2s] | |
| results_df['Mean of estimates'] = [np.nanmean(remove_outliers(x)) for x in parameters] | |
| results_df['SD of estimates'] = [np.nanstd(remove_outliers(x)) for x in parameters] | |
| results_df |
Results of the simulation are shown below. For comparison I also show the results from the paper. Note that I’m running EM algorithm directly on generated series a, so I don’t have parameters alpha of cointegrating vector.
As you can see my implementation doesn’t perform as well as the one used in the paper. Some of the parameters are close to their true values, but the majority of them are not. Also standard deviations that I get are higher than the ones in the paper.
Now let’s try to solve a simpler problem and treat some parameters as known. For example assume we know parameters zeta_2 and var_2 and we want to use EM algorithm to estimate all other parameters. We need to make slight modifications to EM algorithm function which are shown below.
| def em_algorithm(a, max_iter, tol): | |
| ''' | |
| run em algorithm for max_iter iterations or until convergence | |
| ''' | |
| npdf = stats.norm.pdf | |
| converged = False | |
| while not converged: | |
| try: | |
| # random initial guess | |
| ksi = np.random.uniform(-3,3,(3)) | |
| zeta_1 = np.random.uniform(-3,3,(3)) | |
| #zeta_2 = np.random.uniform(-3,3,(2)) | |
| var_1 = np.random.uniform(0,6,(1)) | |
| #var_2 = np.random.uniform(0,6,(1)) | |
| # true values | |
| #ksi = np.array([-1.3,0.6,0.3]) | |
| #zeta_1 = np.array([0,0.6,-0.2]) | |
| zeta_2 = np.array([0,1.5]) | |
| #var_1 = np.array([1]) | |
| var_2 = np.array([3]) | |
| # create dataframe | |
| df = pd.DataFrame(columns=['const', 'a', 'a_l1', 'a_l2', 'abs_l1', 'abs_l2', 'p1', 'p2', | |
| 'tau1', 'tau2', 'e1', 'e2']) | |
| df['a'] = a[2:] | |
| df['a_l1'] = a[1:-1] | |
| df['a_l2'] = a[:-2] | |
| df['abs_l1'] = abs(df['a_l1']) | |
| df['abs_l2'] = abs(df['a_l2']) | |
| df['const'] = 1 | |
| for s in range(max_iter): | |
| # E-step | |
| # solve for mixing probabilities | |
| num = np.exp((df[['const', 'abs_l1', 'abs_l2']] * ksi).sum(axis=1)) | |
| denom = (1 + np.exp((df[['const', 'abs_l1', 'abs_l2']] * ksi).sum(axis=1))) | |
| df['p1'] = num/denom | |
| df['p2'] = 1 - df['p1'] | |
| # calculate e | |
| df['e1'] = df['a'] - (zeta_1 * df[['const', 'a_l1', 'a_l2']]).sum(axis=1) | |
| df['e2'] = df['a'] - (zeta_2 * df[['const', 'a_l1']]).sum(axis=1) | |
| # calculate tau | |
| sigma_1 = np.sqrt(var_1) | |
| sigma_2 = np.sqrt(var_2) | |
| denom = ((df['p1'] / sigma_1) * stats.norm.pdf(df['e1'] / sigma_1) + | |
| (df['p2'] / sigma_2) * stats.norm.pdf(df['e2'] / sigma_2)) | |
| df['tau1'] = (df['p1'] / sigma_1) * stats.norm.pdf(df['e1'] / sigma_1) / denom | |
| df['tau2'] = (df['p2'] / sigma_2) * stats.norm.pdf(df['e2'] / sigma_2) / denom | |
| # M-step | |
| # compute ksi | |
| dr_dksi = df[['const', 'abs_l1', 'abs_l2']] | |
| dQ_dksi = (np.tile((df['tau1'] - df['p1']), (3,1)).T * dr_dksi).sum().values | |
| df['dr_dksi^2'] = df[['const', 'abs_l1', 'abs_l2']].apply(outer, axis=1).apply(np.array) | |
| d2Q_dksi2 = -(df['p1'] * df['p2'] * df['dr_dksi^2']).sum() | |
| new_ksi = ksi - np.linalg.inv(d2Q_dksi2) @ dQ_dksi | |
| # compute zeta | |
| df['de1_dzeta1^2'] = df[['const', 'a_l1', 'a_l2']].apply(outer, axis=1).apply(np.array) | |
| df['de2_dzeta2^2'] = df[['const', 'a_l1']].apply(outer, axis=1).apply(np.array) | |
| zeta1_sum1 = (df['tau1'] * df['de1_dzeta1^2']).sum() | |
| zeta2_sum1 = (df['tau2'] * df['de2_dzeta2^2']).sum() | |
| zeta1_sum2 = (-np.tile(df['tau1'] * df['a'], (3,1)).T * -df[['const', 'a_l1', 'a_l2']]).sum().values | |
| zeta2_sum2 = (-np.tile(df['tau2'] * df['a'], (2,1)).T * -df[['const', 'a_l1']]).sum().values | |
| new_zeta_1 = np.linalg.inv(zeta1_sum1) @ zeta1_sum2 | |
| new_zeta_2 = np.linalg.inv(zeta2_sum1) @ zeta2_sum2 | |
| # compute variance | |
| sigma1_sum2 = (df['tau1'] * (df['a'] + np.dot(-df[['const', 'a_l1', 'a_l2']], new_zeta_1))**2).sum() | |
| sigma2_sum2 = (df['tau2'] * (df['a'] + np.dot(-df[['const', 'a_l1']], new_zeta_2))**2).sum() | |
| new_var_1 = 1/df['tau1'].sum() * sigma1_sum2 | |
| new_var_2 = 1/df['tau2'].sum() * sigma2_sum2 | |
| # calculate the difference between old and new values of parameters | |
| delta_ksi = np.sum(abs(new_ksi - ksi)) | |
| delta_zeta_1 = np.sum(abs(new_zeta_1 - zeta_1)) | |
| delta_zeta_2 = np.sum(abs(new_zeta_2 - zeta_2)) | |
| delta_var_1 = np.sum(abs(new_var_1 - var_1)) | |
| delta_var_2 = np.sum(abs(new_var_2 - var_2)) | |
| # update parameters | |
| ksi = new_ksi | |
| zeta_1 = new_zeta_1 | |
| #zeta_2 = new_zeta_2 | |
| var_1 = new_var_1 | |
| #var_2 = new_var_2 | |
| # calculate total difference between old and new parameters | |
| delta_total = delta_ksi + delta_zeta_1 + delta_var_1 | |
| # check convergence | |
| if delta_total < tol: | |
| print('Converged at iteration ', s) | |
| converged = True | |
| break | |
| # if any parameter is nan, stop | |
| nansum = (np.isnan(ksi).sum() + np.isnan(zeta_1).sum() + np.isnan(zeta_2).sum() + | |
| np.isnan(var_1).sum() + np.isnan(var_2).sum()) | |
| if nansum != 0: | |
| break | |
| if not converged: | |
| print(f'Algorithm not converged') | |
| print('Repeating with different initital values') | |
| except: | |
| continue | |
| # calculate Q | |
| Q_sum1 = (df['tau1'] * (np.log(df['p1']) - 1/2*np.log(var_1) - df['e1']**2 / (2 * var_1))).sum() | |
| Q_sum2 = (df['tau2'] * (np.log(df['p2']) - 1/2*np.log(var_2) - df['e2']**2 / (2 * var_2))).sum() | |
| Q = Q_sum1 + Q_sum2 | |
| return ksi, zeta_1, var_1, zeta_2, var_2, Q |
We don’t make random guesses about parameters zeta_2 and var_2 (lines 15 and 17) and instead use their true values (lines 22 and 24). We don’t update known parameters (lines 94 and 96) and we don’t use them in checking whether the algorithm is converged (line 99). I will also decrease the number of simulations to run to 100 just to save time. Everything else is the same. Results are provided below.
As you can see our estimates are pretty close to the true values of the parameters, which suggests that the formulas for updating those parameters are implemented correctly. Let’s try to repeat this experiment but now treating zeta_1 and var_1 as known.
Again the estimates of unknown parameters are very close to their true values. Now let’s assume that ksi is known.
Here again the estimates are close to true values.
So if some of the parameters are known, other parameters are estimated correctly. But when we try to estimate all the parameters, the accuracy of the estimates drops significantly.
Here is what I tried to fix this:
increasing the number of simulations and the number of datapoints in each simulation
running EM algorithm on each simulated dataset several times with different starting values and selecting results with the highest expected value of the log likelihood (Q)
using sample variance as a starting point for parameters var_1 and var_2
None of the above worked. Clearly something must be wrong in my implementation, but each parameter individually is estimated correctly and the problem only occurs when I try to estimate all parameters together.
For now I don’t know what else to try. If you have any ideas please let me know in the comments.
Jupyter notebook with source code is available here.
If you have any questions, suggestions or corrections please post them in the comments. Thanks for reading.
References
[1] Basket trading under co-integration with the logistic mixture autoregressive model