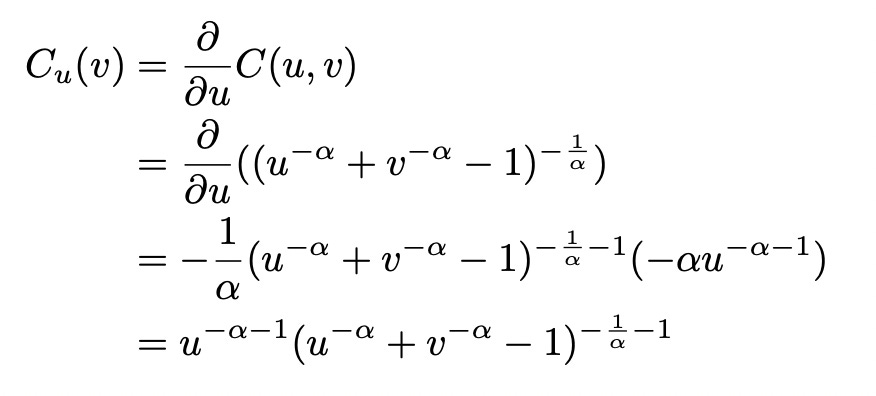Introduction to copulas (Part 2)

Key principles of copulas for quantitative analysis.

Aug 01, 2024

In this article I’m going to describe several more advanced copula functions (compared to the ones described in the previous part). I will consider copulas from Archimedean family — Clayton, Gumbel, Frank and Joe copulas. I will implement them from scratch in Python and show how to sample from them and how to fit them to data.

Archimedean family is probably the most famous class of copulas. Let’s start with a general definition. I will use bivariate version, but it can be easily generalized to higher dimensions. A copula is Archimedean if it can be written in the following form:

So to define an Archimedean copula it is sufficient to provide a generator function phi. The definition above might not be very clear now, but I think it’ll be easy enough to understand after I show a couple of examples.

There are many different types of Archimedean copulas. For example Roger B. Nelsen’s book ‘An introduction to copulas’ lists 22 of them. Let’s start with Clayton copula. The generator function for it is:

Clayton copula generator function

To construct the copula function we need to know the pseudo-inverse of the generator function. We need to derive the value of t as a function of phi:

Now let’s construct Clayton copula function:

The plot of Clayton copula with parameter alpha=6 is presented below.

Now we need to solve two more problems: how to sample from a given copula and how to fit it to data. I will start with sampling.

First sampling technique is based on conditional CDF. The algorithm is quite simple:

Let’s try to apply it to Clayton copula. First we need to calculate conditional CDF:

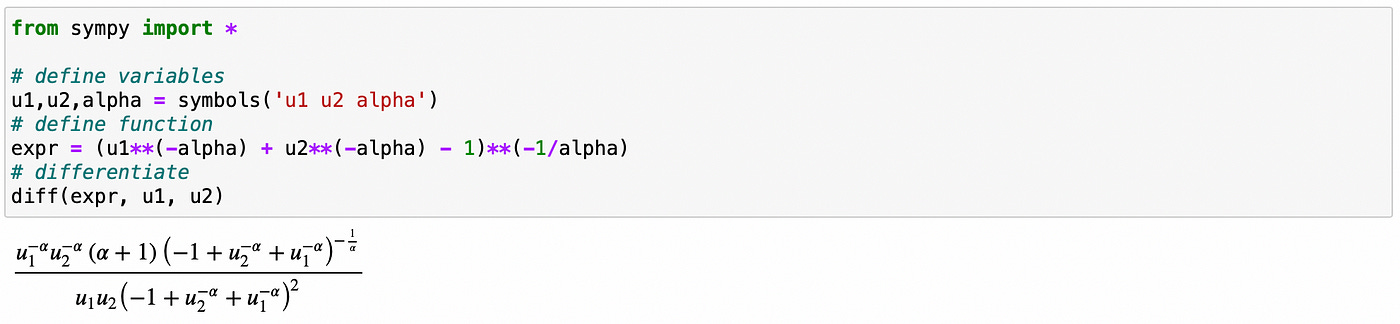
Calculating derivatives can be very time consuming and prone to human errors. Let me show you a way to calculate derivative in Python using sympy library. In the example below we set variable expr equal to the expression for a Clayton copula. We then use diff function to calculate partial derivative of the copula function with respect to variable u. You can easily verify that the expression we get from sympy is identical to the one we calculated above.

Now we need to calculate the inverse of conditional CDF. I don’t know how to do it with sympy, so I’m doing it manually:

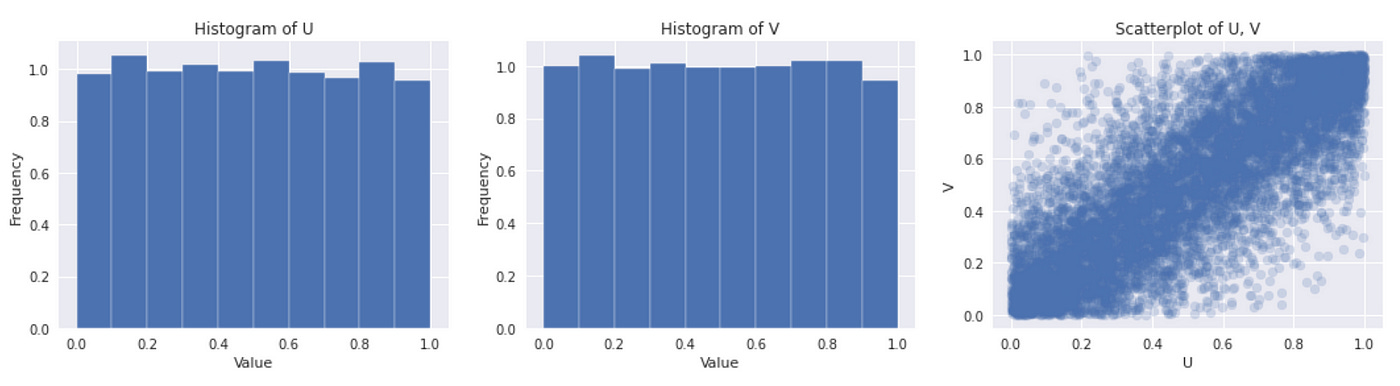
That’s it, we are ready to generate samples from Clayton copula. The code for it is provided below.

This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters

Show hidden characters

	# set parameter
	alpha = 6
	# generate a sample
	u = np.random.rand(10000)
	t = np.random.rand(10000)
	v = ((t / u(-alpha-1))(-alpha/(1+alpha)) - u(-alpha) + 1)(-1/alpha)

	# plot marginals and joint distribution
	fig, ax = plt.subplots(figsize=(18,4), nrows=1, ncols=3)
	ax[0].hist(u, density=True)
	ax[0].set(title='Histogram of U', xlabel='Value', ylabel='Frequency')
	ax[1].hist(v, density=True)
	ax[1].set(title='Histogram of V', xlabel='Value', ylabel='Frequency')
	ax[2].scatter(u, v, alpha=0.2)
	ax[2].set(title='Scatterplot of U, V', xlabel='U', ylabel='V')

view raw clayton_sample_1.py hosted with ❤ by GitHub

On the plot above we can verify that both marginal distributions look like standard uniform.

The method of sampling described above doesn’t always work. Sometimes we can have a conditional CDF that is not directly invertible. Luckily there is another way to sample from an Archimedean copula. It involves using Kendall distribution function, which can be easily constructed from the copula generator function. The general algorithm is presented below:

Let’s try to generate samples from Clayton copula using this method. We can derive a formula for Kendall distribution function using sympy:

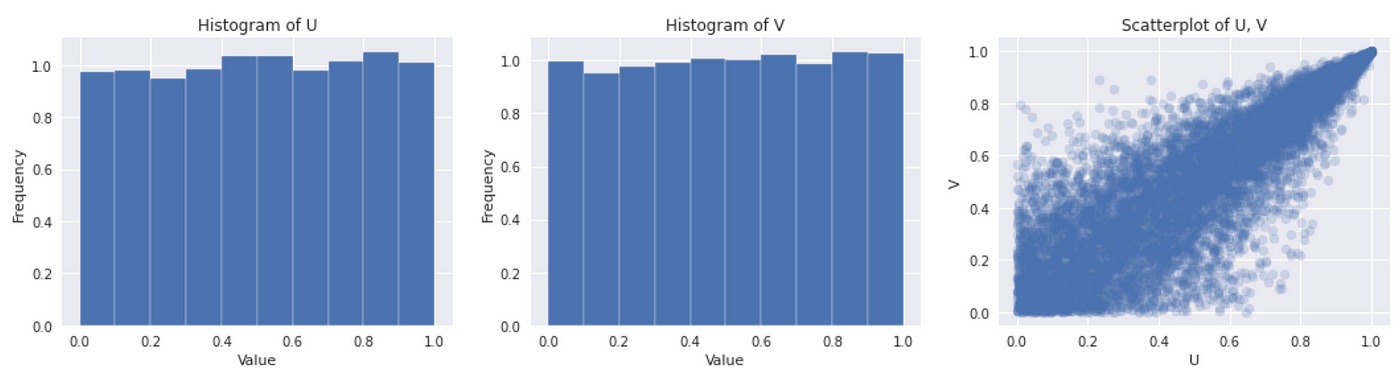
Now we are ready to implement the second sampling method. The source code and the resulting plots are provided below. We implement functions for generator function, inverse generator function and Kendall distribution function. The rest is done according to the algorithm described above.

Show hidden characters

	from scipy.optimize import brentq

	def clayton_phi(t, alpha):
	return 1/alpha * (t**(-alpha) - 1)

	def clayton_phi_inv(t, alpha):
	return (alpha * t + 1)**(-1/alpha)

	def clayton_K(t, alpha):
	return t * (alpha - t**alpha + 1) / alpha

	# set copula parameter
	alpha = 6

	# step 1
	t1 = np.random.rand(10000)
	t2 = np.random.rand(10000)

	# steps 2 and 3
	w = []
	for t in t2:
	func = lambda w: clayton_K(w, alpha=alpha) - t
	w.append(brentq(func, 0.0000000001, 0.9999999999))
	w = np.array(w).flatten()

	# step 4
	u = clayton_phi_inv(t1 * clayton_phi(w, alpha=alpha), alpha=alpha)
	v = clayton_phi_inv((1-t1) * clayton_phi(w, alpha=alpha), alpha=alpha)

	# plot marginals and joint distribution
	fig, ax = plt.subplots(figsize=(18,4), nrows=1, ncols=3)
	ax[0].hist(u, density=True)
	ax[0].set(title='Histogram of U', xlabel='Value', ylabel='Frequency')
	ax[1].hist(v, density=True)
	ax[1].set(title='Histogram of V', xlabel='Value', ylabel='Frequency')
	ax[2].scatter(u, v, alpha=0.2)
	ax[2].set(title='Scatterplot of U, V', xlabel='U', ylabel='V')

view raw clayton_sample_2.py hosted with ❤ by GitHub

As we can see on the plots above, the results we get are similar to what we got using another method. I think this method is more universal and easier to use. Derivative of the generator function is usually easier to calculate than the derivative of the copula function. So I will use this technique for other copulas. But before we explore other copulas let’s see how to fit copula to data.

There are several methods available for copula parameter estimation. I will consider two of them: estimation based on dependence measures (such as Spearman’s rho or Kendall’s tau) and Canonical Maximum Likelihood (CML).

For some copulas there is an analytical formula for computing its parameter based on a dependence measure. So we can just calculate this dependence measure for our data and plug it into the formula to get the parameter value. A couple of examples:

In the formulas above tau is Kendall rank correlation coefficient.

Let’s see how this works in practice. I will use Clayton copula we generated above to get a sample of two variables — one with normal distribution, another with exponential distribution. Then I’ll calculate Kendall’s tau for these variables, plug it into the formula above and compare with the real value of alpha I used to generate the copula.

Show hidden characters

	# define distributions
	dist_x = stats.norm()
	dist_y = stats.expon()
	# transform
	x = dist_x.ppf(u)
	y = dist_y.ppf(v)
	# calculate tau
	tau = stats.kendalltau(x,y)[0]
	# calculate alpha
	clayton_alpha = 2 * tau / (1 - tau)
	clayton_alpha

view raw fit_tau.py hosted with ❤ by GitHub

We get alpha=6.18, which is very close to the true value of 6. The method works as expected, but there is a problem — for most copulas there is no analytical solution available. So this technique will work only for a limited number of copulas.

The other method (CML) is a little more difficult, but it is also more versatile. The idea is simple: transform variables to uniform using probability integral transform and then select the value of parameter alpha that maximizes the log-likelihood function of the copula. The most difficult part here is calculating the copula Probability Density Function (PDF), which is necessary to define log-likelihood function. But this task can be simplified using sympy. PDF of bivariate copula can be calculated from its CDF as follows:

It can be easily done in Python with sympy:

Now we are ready implement CML. Look at the code below. I’m using the same variables (x and y) that we generated before.

Show hidden characters

	from scipy.optimize import minimize_scalar

	def clayton_pdf(u1, u2, alpha):
	num = u1*(-alpha) u2*(-alpha) (alpha+1) * (-1 + u2(-alpha) + u1(-alpha))**(-1/alpha)
	denom = u1 * u2 * (-1 + u2(-alpha) + u1(-alpha))**2
	return num/denom

	def clayton_neg_likelihood(alpha, u1, u2):
	return -np.sum(np.log(clayton_pdf(u1,u2,alpha)))

	minimize_scalar(clayton_neg_likelihood, args=(dist_x.cdf(x), dist_y.cdf(y)),
	bounds=(-1,20), method='bounded')

view raw clayton_fit_cml.py hosted with ❤ by GitHub

Note that in the code above I’m defining negative log-likelihood function. The reason for this is that we are using minimize_scalar function, which minimizes a given expression. Minimizing negative log-likelihood is equal to maximizing log-likelihood. You can see the results below.

The estimated value of the parameter is close to the true value used to generate given data, so everything works as expected.

Now we have all the necessary building blocks for creating other Archimedean copulas, sampling from them and fitting them to data. Let me demonstrate it on several examples.

Gumbel copula

For Gumbel copula we have:

I’m going to generate a sample from Gumbel copula using Kendall distribution function. Code for it along with resulting plots is provided below.

Show hidden characters

	def gumbel_phi(t, alpha):
	return (-np.log(t))**alpha

	def gumbel_phi_inv(t, alpha):
	return np.exp(-t**(1/alpha))

	def gumbel_K(t, alpha):
	return t * (alpha - np.log(t)) / alpha

	alpha = 5.6
	t1 = np.random.rand(10000)
	t2 = np.random.rand(10000)

	w = []
	for t in t2:
	func = lambda w: gumbel_K(w, alpha=alpha) - t
	w.append(brentq(func, 0.0000000001, 0.9999999999))
	w = np.array(w).flatten()

	u = gumbel_phi_inv(t1 * gumbel_phi(w, alpha=alpha), alpha=alpha)
	v = gumbel_phi_inv((1-t1) * gumbel_phi(w, alpha=alpha), alpha=alpha)

	# plot marginals and joint distribution
	fig, ax = plt.subplots(figsize=(18,4), nrows=1, ncols=3)
	ax[0].hist(u, density=True)
	ax[0].set(title='Histogram of U', xlabel='Value', ylabel='Frequency')
	ax[1].hist(v, density=True)
	ax[1].set(title='Histogram of V', xlabel='Value', ylabel='Frequency')
	ax[2].scatter(u, v, alpha=0.2)
	ax[2].set(title='Scatterplot of U, V', xlabel='U', ylabel='V')

view raw gumbel_sample.py hosted with ❤ by GitHub

Gumbel copula is one of a few copula families for which there is an analytic formula connecting parameter alpha to Kendall’s tau. I’m using the same technique to generate some data from Gumbel copula as I used before.

As you can see on the picture above we get 5.58 which is very close to the true value of 5.6.

Implementing the CML method involves differentiating a CDF function, which is not so easy to do. Luckily we have sympy. Below I define Gumbel copula function and calculate its derivative using sympy.

Using the above formula we can now define gumbel_pdf and gumbel_neg_likelihood functions.

Show hidden characters

	def gumbel_pdf(u1, u2, alpha):
	num1 = (-np.log(u1))*alpha (-np.log(u2))*alpha ((-np.log(u1))alpha + (-np.log(u2))alpha)**(1/alpha)
	num2 = alpha + ((-np.log(u1))alpha + (-np.log(u2))alpha)**(1/alpha) - 1
	num3 = np.exp(-((-np.log(u1))alpha + (-np.log(u2))alpha)**(1/alpha))
	denom = u1 * u2 * ((-np.log(u1))alpha + (-np.log(u2))alpha)*2 np.log(u1) * np.log(u2)

	return (num1 * num2 * num3) / denom

	def gumbel_neg_likelihood(alpha, u1, u2):
	return -np.sum(np.log(gumbel_pdf(u1,u2,alpha)))

	minimize_scalar(gumbel_neg_likelihood, args=(dist_x.cdf(x), dist_y.cdf(y)),
	bounds=(-1,20), method='bounded')

view raw gumbel_fit_cml.py hosted with ❤ by GitHub

As you can see above, CML gives a number which is close to the true value of 5.6.

Frank copula

To construct Frank copula we use the following formulas:

Source code for sampling from Frank copula and the resulting plots are shown below.

Show hidden characters

	def frank_phi(t, alpha):
	return -np.log((np.exp(-alpha*t) - 1) / (np.exp(-alpha) - 1))

	def frank_phi_inv(t, alpha):
	return -1/alpha * np.log((np.exp(-alpha) - 1) / np.exp(t) + 1)

	def frank_K(t, alpha):
	return (t + (1 - np.exp(alphat)) np.log((1-np.exp(alphat))
	np.exp(-alpha*t+alpha) / (1-np.exp(alpha))) / alpha)

	alpha = 8
	t1 = np.random.rand(10000)
	t2 = np.random.rand(10000)

	w = []
	for t in t2:
	func = lambda w: frank_K(w, alpha=alpha) - t
	w.append(brentq(func, 0.0000000001, 0.9999999999))
	w = np.array(w).flatten()

	u = frank_phi_inv(t1 * frank_phi(w, alpha=alpha), alpha=alpha)
	v = frank_phi_inv((1-t1) * frank_phi(w, alpha=alpha), alpha=alpha)

	# plot marginals and joint distribution
	fig, ax = plt.subplots(figsize=(18,4), nrows=1, ncols=3)
	ax[0].hist(u, density=True)
	ax[0].set(title='Histogram of U', xlabel='Value', ylabel='Frequency')
	ax[1].hist(v, density=True)
	ax[1].set(title='Histogram of V', xlabel='Value', ylabel='Frequency')
	ax[2].scatter(u, v, alpha=0.2)
	ax[2].set(title='Scatterplot of U, V', xlabel='U', ylabel='V')

view raw frank_sample.py hosted with ❤ by GitHub

To fit Frank copula to data we need to calculate its PDF, which I do using sympy.

Note that here I use simplify function from sympy to get a simpler expression, which is easier to type when defining a PDF function.

Everything else is exactly the same as before. Define PDF and log-likelihood functions and run optimizer to search for parameter value that maximizes log-likelihood.

Show hidden characters

	def frank_pdf(u1, u2, alpha):
	num = alpha * (np.exp(alpha) - 1) * np.exp(alpha * (u1 + u2 + 1))
	denom = (-(np.exp(alpha) - 1) * np.exp(alpha * (u1 + u2)) +
	(np.exp(alphau1)-1) (np.exp(alphau2)-1) np.exp(alpha))**2
	return num/denom

	def frank_neg_likelihood(alpha, u1, u2):
	return -np.sum(np.log(frank_pdf(u1,u2,alpha)))

	# define distributions
	dist_x = stats.norm()
	dist_y = stats.expon()
	# transform
	x = dist_x.ppf(u)
	y = dist_y.ppf(v)

	minimize_scalar(frank_neg_likelihood, args=(dist_x.cdf(x), dist_y.cdf(y)),
	bounds=(-20,20), method='bounded')

view raw frank_fit.py hosted with ❤ by GitHub

And again we get correct results. Let’s look at one last example.

Joe copula

Formulas:

Sampling:

Show hidden characters

	def joe_phi(t, alpha):
	return -np.log(1 - (1-t)**alpha)

	def joe_phi_inv(t, alpha):
	return 1 - (1 - np.exp(-t))**(1/alpha)

	def joe_K(t, alpha):
	return 1/alpha * (1-t)*(-alpha) (alphat(1-t)*alpha - (t-1) ((1-t)*alpha-1) np.log(1 - (1-t)**alpha))

	alpha = 5
	t1 = np.random.rand(10000)
	t2 = np.random.rand(10000)

	w = []
	for t in t2:
	func = lambda w: joe_K(w, alpha=alpha) - t
	w.append(brentq(func, 0.0000000001, 0.9999999999))
	w = np.array(w).flatten()

	u = joe_phi_inv(t1 * joe_phi(w, alpha=alpha), alpha=alpha)
	v = joe_phi_inv((1-t1) * joe_phi(w, alpha=alpha), alpha=alpha)

	# plot marginals and joint distribution
	fig, ax = plt.subplots(figsize=(18,4), nrows=1, ncols=3)
	ax[0].hist(u, density=True)
	ax[0].set(title='Histogram of U', xlabel='Value', ylabel='Frequency')
	ax[1].hist(v, density=True)
	ax[1].set(title='Histogram of V', xlabel='Value', ylabel='Frequency')
	ax[2].scatter(u, v, alpha=0.2)
	ax[2].set(title='Scatterplot of U, V', xlabel='U', ylabel='V')

view raw joe_sample.py hosted with ❤ by GitHub

Fitting:

Note that the simplified expression above doesn’t fit on my screen and therefore it is not shown in full. Check Jupiter notebook (link provided in the end of the article) to see the whole expression.

Show hidden characters

	def joe_pdf(u1, u2, alpha):
	# fix numerical issues:
	u1[u1==1] = 0.999999999
	u1[u1==0] = 0.000000001
	u2[u2==1] = 0.999999999
	u2[u2==0] = 0.000000001

	n1 = (1-u1)*(alpha-1) (1-u2)**(alpha-1)
	n2 = (-(1-u1)*alpha (1-u2)alpha + (1-u1)alpha + (1-u2)alpha) (-2 + 1/alpha)
	n3 = (alpha * ((1-u1)*alpha - 1) ((1-u2)*alpha - 1) + alpha(-(1-u1)*alpha (1-u2)**alpha +
	(1-u1)alpha + (1-u2)alpha) - ((1-u1)*alpha-1) ((1-u2)**alpha - 1))
	return n1 * n2 * n3

	def joe_neg_likelihood(alpha, u1, u2):
	return -np.sum(np.log(joe_pdf(u1,u2,alpha)))

	# define distributions
	dist_x = stats.norm()
	dist_y = stats.expon()
	# transform
	x = dist_x.ppf(u)
	y = dist_y.ppf(v)

	minimize_scalar(joe_neg_likelihood, args=(dist_x.cdf(x), dist_y.cdf(y)),
	bounds=(1,20), method='bounded')

view raw joe_fit.py hosted with ❤ by GitHub

Here I had to make a little change in the pdf function because I encountered some numerical issues. Basically we need to make sure that none of the elements in arrays u1,u2 are exactly equal to 0 or 1.

As you can see above, the result we get is correct.

I hope that everything was clear and now you can implement any other Archimedean copula on your own. In the next article I will try to apply this knowledge in practice and implement a pairs trading strategy using copulas.

Jupyter notebook with source code is available here.

If you have any questions, suggestions or corrections please post them in the comments. Thanks for reading.

Financial Noob

Discussion about this post