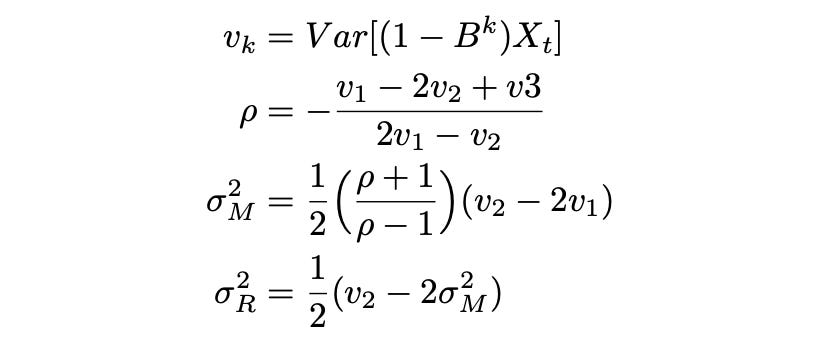This article is based on the paper ‘Modeling Time Series with both Permanent and Transient Components using the Partially Autoregressive Model’ (Clegg et al. 2015). I am going to describe the model from that paper, show how to implement provided estimation techniques in Python and try to replicate some studies using both synthetic and real data.
Partial autoregressive (PAR) model is proposed to describe time series, which have both permanent and transient components. It can be described with following equations:
Time series X_t consists of two components — random walk component R_t (permanent) and mean-reverting component M_t (transient), where rho is the coefficient of mean reversion.
Authors claim that:
the model presented in equation (1) is perhaps the simplest possible model having both a mean-reverting and a random walk component. This makes it the natural starting point for a study of such time series.
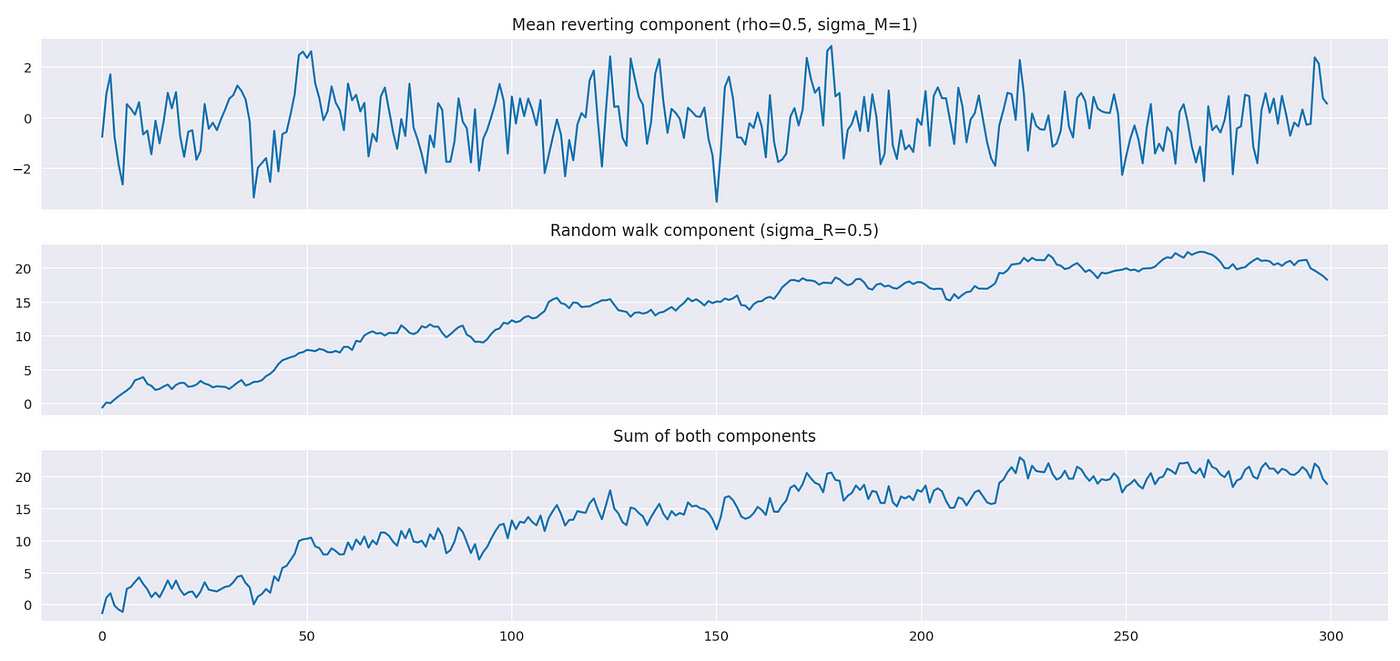
Let’s try to generate and plot a sample from PAR model to see how it looks. Code for it is shown below.
| N = 300 # number of datapoints | |
| sigma_M = 1 | |
| sigma_R = 0.5 | |
| rho = 0.5 | |
| from statsmodels.tsa.arima_process import arma_generate_sample | |
| np.random.seed(44) | |
| ar_M = np.r_[1, -rho] | |
| ar_R = np.r_[1, -1] | |
| ma = np.r_[1] | |
| M = arma_generate_sample(ar_M, ma, N, scale=sigma_M) | |
| R = arma_generate_sample(ar_R, ma, N, scale=sigma_R) | |
| X = M + R | |
| fig, (ax1,ax2,ax3) = plt.subplots(3, 1, figsize=(18,8), sharex=True) | |
| ax1.plot(M) | |
| ax1.set_title(f'Mean reverting component (rho={rho}, sigma_M={sigma_M})') | |
| ax2.plot(R) | |
| ax2.set_title(f'Random walk component (sigma_R={sigma_R})') | |
| ax3.plot(X) | |
| ax3.set_title('Sum of both components') |
First we set model parameters — rho, sigma_M, sigma_R, and number of datapoints we want to generate. Then we generate each component separately, according to model specification presented above. After that we just sum the two components to get a sample from PAR model. To generate mean reverting and random walk components I’m using a function from statsmodels library. Documentation for it is available here.
Above you can see the plots of both components and of resulting time series. Note that the bottom plot closely resembles the random walk component, with some additional noise from mean reverting component.
We can check that the empirical parameters calculated from the sample are close to the real ones.
Another interesting metric we can calculate is the proportion of variance attributable to mean reversion. Formula for it is provided below.
The results of this calculation are shown on the screenshot below.
I am going implement functions based on the code we used so far. One function to generate a PAR sample and another to calculate R squared.
| def generate_par(N, rho, sigma_M, sigma_R): | |
| ''' | |
| Generate PAR sample of length N with parameters rho, sigma_M, sigma_R | |
| ''' | |
| from statsmodels.tsa.arima_process import arma_generate_sample | |
| ar_M = np.r_[1, -rho] | |
| ar_R = np.r_[1, -1] | |
| ma = np.r_[1] | |
| M = arma_generate_sample(ar_M, ma, N, scale=sigma_M) | |
| R = arma_generate_sample(ar_R, ma, N, scale=sigma_R) | |
| return M+R | |
| def calculate_Rsq(rho, sigma_M, sigma_R): | |
| ''' | |
| Calculate R^2 - proportion of variance attributable to mean reversion | |
| ''' | |
| return (2*sigma_M**2) / (2*sigma_M**2 + (1+rho) * sigma_R**2) |
Now we can try estimating the model parameters. First method proposed by the authors is using lagged variances. It doesn’t work very well for small sample sizes, but it’s a good starting point. Formulas and code for calculating model parameters are provided below.
| # generate a sample | |
| N = 2500 | |
| sigma_M = 1 | |
| sigma_R = 0.5 | |
| rho = 0.5 | |
| np.random.seed(44) | |
| X = generate_par(N, rho, sigma_M, sigma_R) | |
| # calculate lagged variances | |
| v1 = np.var(X[1:] - X[:-1]) | |
| v2 = np.var(X[2:] - X[:-2]) | |
| v3 = np.var(X[3:] - X[:-3]) | |
| # rho | |
| rho_lv = -(v1 - 2*v2 + v3) / (2*v1 - v2) | |
| # sigma_M | |
| sigma_M_lv = np.sqrt(1/2 * (rho_lv+1) / (rho_lv-1) * (v2 - 2*v1)) | |
| # sigma_R | |
| sigma_R_lv = np.sqrt(1/2 * (v2 - 2*sigma_M_lv**2)) |
As you can see above, with large enough sample size we are able to get estimates that are pretty close to the true values of the parameters.
Let’s create a function for estimating parameters of the model using lagged variances. Note that when calculating variances we need to check that the value under the square root is non-negative, otherwise we will get an error.
| def lagvar_estimate_par(X): | |
| ''' | |
| estimate parameters of partial AR model using lagged variances | |
| ''' | |
| # calculate lagged variances | |
| v1 = np.var(X[1:] - X[:-1]) | |
| v2 = np.var(X[2:] - X[:-2]) | |
| v3 = np.var(X[3:] - X[:-3]) | |
| # rho | |
| rho_lv = -(v1 - 2*v2 + v3) / (2*v1 - v2) | |
| # sigma_M | |
| if (rho_lv+1) / (rho_lv-1) * (v2 - 2*v1) > 0: | |
| sigma_M_lv = np.sqrt(1/2 * (rho_lv+1) / (rho_lv-1) * (v2 - 2*v1)) | |
| else: | |
| sigma_M_lv = 0 | |
| # sigma_R | |
| if v2 > 2*sigma_M_lv**2: | |
| sigma_R_lv = np.sqrt(1/2 * (v2 - 2*sigma_M_lv**2)) | |
| else: | |
| sigma_R_lv = 0 | |
| return rho_lv, sigma_M_lv, sigma_R_lv |
Another estimation technique proposed in the paper is based on the Maximum Likelihood Estimation (MLE) of the Kalman filter. We reformulate the PAR model in a state-space form and design a Kalman filter for it. Then we maximize the corresponding log-likelihood function with respect to the parameters of the model (rho, sigma_M, sigma_R). You can learn more about state space models and Kalman filters in my other article.
Let’s try to implement this procedure step by step. First we need to write a function for Kalman filtering. Code for the function in R language is provided in the paper, I’m just rewriting it in Python with some minor changes. Note that additionally to mean reverting and random walk components (M and R) my function also returns prediction errors eps because they are needed for log-likelihood function.
| def kalman_estimate(X, rho, sigma_M, sigma_R): | |
| ''' | |
| Calculate estimates of mean-reverting and random walk components | |
| ''' | |
| # create arrays for storing both components and prediction errors | |
| M = np.zeros(len(X)) | |
| R = np.zeros(len(X)) | |
| eps = np.zeros(len(X)) | |
| # set initial state | |
| if sigma_R==0: | |
| M[0] = X[0] | |
| R[0] = 0 | |
| else: | |
| M[0] = 0 | |
| R[0] = X[0] | |
| # calculate Kalman gain | |
| if sigma_M==0: | |
| K_M = 0 | |
| K_R = 1 | |
| elif sigma_R==0: | |
| K_M = 1 | |
| K_R = 0 | |
| else: | |
| sqr = np.sqrt((1+rho)**2 * sigma_R**2 + 4*sigma_M**2) | |
| K_M = 2*sigma_M**2 / (sigma_R * (sqr + rho*sigma_R + sigma_R) + 2*sigma_M**2) | |
| K_R = 2*sigma_R / (sqr - rho*sigma_R + sigma_R) | |
| # calculate estimates | |
| for i in range(1, len(X)): | |
| xhat = rho * M[i-1] + R[i-1] | |
| eps[i] = X[i] - xhat | |
| M[i] = rho * M[i-1] + eps[i] * K_M | |
| R[i] = R[i-1] + eps[i] * K_R | |
| return M, R, eps |
When parameters of the PAR model are known, we can apply Kalman filter to the data and get estimates of the components and prediction errors. Having calculated prediction errors, we can calculate log-likelihood as follows.
Initially parameters of the model are not known to us. We use lagged variances method to calculate our initial estimates. Then we use numerical optimization methods (quasi-Newton) to obtain parameter values that maximize the log-likelihood function. Let’s see how it is implemented in code.
We need to implement a function to calculate the log-likelihood. Code for it is shown below.
| def log_like(X, rho, sigma_M, sigma_R): | |
| ''' | |
| Compute log likelihood function | |
| ''' | |
| N = len(X) | |
| _,_,eps = kalman_estimate(X, rho, sigma_M, sigma_R) | |
| ll = -(N-1)/2 * np.log(2*np.pi * (sigma_M**2 + sigma_R**2)) - 1 / (2 * (sigma_M**2 + sigma_R**2)) * np.sum(eps[1:]**2) | |
| return ll |
I am going to use scipy library to perform numerical optimization. Objective function, that we are going to minimize, should follow a certain template (see here), so let’s create a function that we are going to pass to scipy minimize.
| def f_to_min_par(parameters, X): | |
| rho, sigma_M, sigma_R = parameters | |
| return -log_like(X, rho, sigma_M, sigma_R) |
First argument of the objective function indicates the parameters, with respect to which the function must be minimized. Second argument contains our data. We want to maximize the likelihood function, which is the same as minimizing the negative likelihood function.
Let’s see how this estimation technique works from the beginning. First we generate a sample with given parameters, as shown in the code below. Here we don’t need a very big sample, so I’m generating just 250 datapoints.
| # generate a sample | |
| N = 250 | |
| rho = 0.7 | |
| sigma_M = 1 | |
| sigma_R = 0.5 | |
| np.random.seed(11) | |
| X = generate_par(N, rho, sigma_M, sigma_R) |
Then we use lagged variances method to get initial estimates of the parameters. Results are shown on a screenshot.
As you can see above, the estimates are not very accurate. Let’s see if we can get better estimates with maximum likelihood estimation. Code for performing MLE is shown below along with the results. The numbers we get are closer to the true values than our initial estimates.
Now we are ready to create a function implementing this estimation technique and perform some tests using synthetic data.
There are two special cases of the PAR model that we need to keep in mind during implementation. The first one is pure random walk model, which occurs when sigma_M=0. And the second one is pure mean reverting model, which occurs when sigma_R=0. We can still use the same estimation techniques, we just need to explicitly set the respective parameter to zero. The code for parameter estimation in these special cases is shown below.
| def lagvar_estimate_rw(X): | |
| ''' | |
| estimate parameters of randow walk model using lagged variances | |
| ''' | |
| # calculate lagged variances | |
| v1 = np.var(X[1:] - X[:-1]) | |
| v2 = np.var(X[2:] - X[:-2]) | |
| v3 = np.var(X[3:] - X[:-3]) | |
| # rho | |
| rho_lv = 0 | |
| # sigma_M | |
| sigma_M_lv = 0 | |
| # sigma_R | |
| sigma_R_lv = np.sqrt(1/2 * (v2 - 2*sigma_M_lv**2)) | |
| return sigma_R_lv | |
| def lagvar_estimate_ar(X): | |
| ''' | |
| estimate parameters of AR model using lagged variances | |
| ''' | |
| # calculate lagged variances | |
| v1 = np.var(X[1:] - X[:-1]) | |
| v2 = np.var(X[2:] - X[:-2]) | |
| v3 = np.var(X[3:] - X[:-3]) | |
| # rho | |
| rho_lv = -(v1 - 2*v2 + v3) / (2*v1 - v2) | |
| # sigma_M | |
| if (rho_lv+1) / (rho_lv-1) * (v2 - 2*v1) > 0: | |
| sigma_M_lv = np.sqrt(1/2 * (rho_lv+1) / (rho_lv-1) * (v2 - 2*v1)) | |
| else: | |
| sigma_M_lv = 0 | |
| return rho_lv, sigma_M_lv |
We also need to create different objective functions to use in numerical optimization. Code is provided below.
| def f_to_min_rw(sigma_R, X): | |
| rho = 0 | |
| sigma_M = 0 # remove mean-reverting component | |
| return -log_like(X, rho, sigma_M, sigma_R) | |
| def f_to_min_ar(parameters, X): | |
| rho, sigma_M = parameters | |
| sigma_R = 0 # remove random walk component | |
| return -log_like(X, rho, sigma_M, sigma_R) |
Sometimes using estimates calculated from lagged variances as initial guesses leads to suboptimal results.
Now are ready to write a function for MLE estimation.
| from scipy import stats | |
| def mle_fit(X, mode, tol=0.001): | |
| ''' | |
| fit model using MLE | |
| ''' | |
| estimates = [] | |
| lls = [] | |
| # distribution for random guesses | |
| rnd_rho = stats.uniform(loc=-1, scale=2) | |
| if mode=='PAR': | |
| # get initial guesses using lagged variances | |
| x0 = lagvar_estimate_par(X) | |
| # set boundaries | |
| bounds = ((-1,1), (0,np.inf), (0,np.inf)) | |
| # function to use in minimization | |
| f_to_min = f_to_min_par | |
| # function to generate random initial values | |
| std = np.std(np.diff(X)) | |
| rnd_sigma = stats.norm(loc=std, scale=std/2) | |
| def gen_x0(): | |
| return rnd_rho.rvs(), rnd_sigma.rvs(), rnd_sigma.rvs() | |
| elif mode=='AR': | |
| x0 = lagvar_estimate_ar(X) | |
| bounds = ((-1,1), (0,np.inf)) | |
| f_to_min = f_to_min_ar | |
| std = np.std(np.diff(X)) | |
| rnd_sigma = stats.norm(loc=std, scale=std/2) | |
| def gen_x0(): | |
| return rnd_rho.rvs(), rnd_sigma.rvs() | |
| elif mode=='RW': | |
| x0 = lagvar_estimate_rw(X) | |
| bounds = ((0,np.inf),) | |
| f_to_min = f_to_min_rw | |
| std = np.std(np.diff(X)) | |
| rnd_sigma = stats.norm(loc=std, scale=std/2) | |
| def gen_x0(): | |
| return rnd_sigma.rvs() | |
| # minimize | |
| res = minimize(f_to_min, (x0), args=(X), bounds=bounds, tol=tol) | |
| if res.success: | |
| estimates.append(res.x) | |
| lls.append(-res.fun) # save log-likelihood | |
| # repeat minimization with different (random) initial values | |
| n_att = 0 | |
| while len(lls)<10 and n_att<100: | |
| n_att += 1 | |
| x0 = gen_x0() | |
| res = minimize(f_to_min, (x0), args=(X), bounds=bounds, tol=tol) | |
| if res.success: | |
| estimates.append(res.x) | |
| lls.append(-res.fun) # save log-likelihood | |
| try: | |
| argmax = np.argmax(lls) # index of the biggest likelihood | |
| return estimates[argmax] | |
| except: | |
| #print('Estimation failed!') | |
| return len(x0)*[np.nan] # return nans |
Note that I am repeating the minimization procedure 10 times and return the parameters which give the biggest log-likelihood function. The reason for doing this is that numerical minimization procedure only guarantees that we will find a local minimum. To increase our chances of finding a global minimum we repeat the procedure several times with different initial values and return the best estimates out of all attempts.
Let’s perform some tests of the function to make sure it works as expected. Code for testing the function and plotting results is demonstrated below. Library tqdm imported in the beginning is used for showing a progress bar to monitor progression of the test.
| from tqdm import tqdm | |
| rho = 0.7 | |
| sigma_M = 1 | |
| sigma_R = 0.5 | |
| rhos = [] | |
| sigmaMs = [] | |
| sigmaRs = [] | |
| N_sim = 1000 | |
| N = 500 | |
| with warnings.catch_warnings(): | |
| warnings.simplefilter('ignore') | |
| for i in tqdm(range(N_sim)): | |
| np.random.seed(i) | |
| sample = generate_par(N, rho, sigma_M, sigma_R) | |
| params = mle_fit(sample, mode='PAR') | |
| rhos.append(params[0]) | |
| sigmaMs.append(params[1]) | |
| sigmaRs.append(params[2]) | |
| fig, (ax1,ax2,ax3) = plt.subplots(1, 3, figsize=(18,4)) | |
| ax1.hist(rhos, bins=25, label='Estimates') | |
| ax1.set_title('Estimates of rho') | |
| ax1.axvline(x=rho, label='True value', c='r') | |
| ax1.legend() | |
| ax2.hist(sigmaMs, bins=25, label='Estimates') | |
| ax2.set_title('Estimates of sigma_M') | |
| ax2.axvline(x=sigma_M, label='True value', c='r') | |
| ax2.legend() | |
| ax3.hist(sigmaRs, bins=25, label='Estimates') | |
| ax3.set_title('Estimates of sigma_R') | |
| ax3.axvline(x=sigma_R, label='True value', c='r') | |
| ax3.legend() |
As you can see above, most estimates are concentrated around true values of parameters, which means that our estimation function works as expected. I also tested it in other modes (assuming either sigma_M or sigma_R equals to zero) and it works as expected. Results are available in Jupyter notebook.
I have failed to replicate the simulation studies with the likelihood ratio tests. For some reason my critical values are too different from the ones, provided in the paper. I believe it has something to do with particular implementation of the numerical optimization procedure. In some cases it might not converge to the true global minimum, resulting in outliers that shift the quantiles in wrong direction. Even in the paper, quantiles from the simulation are different from the ones predicted by Wilks’ theorem. I will leave the code for simulation studies in the Jupyter notebook, but I won’t post it here.
Instead of relying on likelihood ratio test, I’m going to use Akaike Information Criterion (AIC) to determine which model better describes the data. Some statisticians even suggest that this approach is better than using statistical tests (e.g. here).
I will try to fit PAR model to real world data. I am going to use the prices of some small cap stocks from 2002 to 2014. Similarly to the paper, I will divide the dataset into six non-overlapping periods (2 years each). For each time series 3 different models will be tested — PAR, pure mean reversion (AR(1) with |rho|<1) and pure random walk. Out of 3 models, the one with the smallest AIC will be selected. For time series, which are identified as PAR, average values of mean reversion coefficient rho and average proportion of variance attributable to mean reversion will be calculated.
First let’s try to work with simple price series. Code for doing it is provided below.
| start_years = [2002, 2004, 2006, 2008, 2010, 2012] | |
| columns = ['AIC_AR', 'AIC_RW', 'AIC_PAR', 'rho', 'sigma_M', 'sigma_R', '$R^2_{MR}$'] | |
| results = {} | |
| with warnings.catch_warnings(): | |
| warnings.simplefilter('ignore') | |
| for sy in start_years: | |
| print(f'Processing years {sy}-{sy+1}') | |
| data_tmp = data.loc[f'{sy}-01-01':f'{sy+2}-01-01'] | |
| data_tmp = data_tmp.dropna(axis=1) | |
| results_df = pd.DataFrame(columns=columns, index=data_tmp.columns) | |
| for s in tqdm(data_tmp.columns): | |
| X = data_tmp[s].values | |
| # fit PAR | |
| rho_par, sigmaM_par, sigmaR_par = mle_fit(X, mode='PAR') | |
| ll_par = log_like(X, rho_par, sigmaM_par, sigmaR_par) | |
| aic_par = 2*3 - 2*ll_par | |
| # fit AR | |
| rho_ar, sigmaM_ar = mle_fit(X, mode='AR') | |
| ll_ar = log_like(X, rho_ar, sigmaM_ar, 0) | |
| aic_ar = 2*2 - 2*ll_ar | |
| # fit RW | |
| sigmaR_rw = mle_fit(X, mode='RW') | |
| ll_rw = log_like(X, 0, 0, sigmaR_rw) | |
| aic_rw = 2*1 - 2*ll_rw | |
| # calculate R^2 | |
| r_sq = calculate_Rsq(rho_par, sigmaM_par, sigmaR_par) | |
| results_df.loc[s] = [aic_ar, aic_rw, aic_par, rho_par, sigmaM_par, sigmaR_par, r_sq] | |
| results[sy] = results_df |
As you can see on the screenshot above, approximately 30–40% of time series are found to be PAR. The average percentage of variance attributable to mean reversion is less than 50% in all periods except one, where it is only slightly bigger than 50%. Let’s try to test the persistence of PAR property — given that the time series is PAR in the current period, how likely is it to be PAR in the next period? I am going to construct a table similar to table 5 in the paper.
| per_col = ['$N$', '$A_{t}$', '$A_{t-1}$', '$A_{t}|A_{t-1}$', '$p_t$', '$p_{t|t-1}$'] | |
| per_ind = sum_ind[1:] | |
| per_df = pd.DataFrame(index=per_ind, columns=per_col) | |
| for i in range(1,len(start_years)): | |
| cur_res = results[start_years[i]] | |
| prev_res = results[start_years[i-1]] | |
| N = len(cur_res) | |
| # calculate A_t | |
| cond = (cur_res['AIC_PAR'] == cur_res[['AIC_AR', 'AIC_RW', 'AIC_PAR']].min(axis=1)) | |
| cur_symbols = cur_res[cond].index # stocks that are PAR in current period | |
| at0 = len(cur_symbols) | |
| # calculaye A_{t-1} | |
| cond = (prev_res['AIC_PAR'] == prev_res[['AIC_AR', 'AIC_RW', 'AIC_PAR']].min(axis=1)) | |
| prev_symbols = prev_res[cond].index # stocks that are PAR in previous period | |
| at1 = len(prev_symbols) | |
| # calculate A_{t}|A_{t-1} | |
| symbols_is = set(cur_symbols).intersection(set(prev_symbols)) | |
| at_is = len(symbols_is) | |
| p0 = at0 / N | |
| p1 = at_is / at1 | |
| sy = start_years[i] | |
| per_df.loc[f'{sy}-{sy+1}'] = [N, at0, at1, at_is, p0, p1] |
As you can see in the last two columns above, time series in the current period is about 1.5 times as likely to be PAR if it was found to be PAR in the previous time period. Results in the paper look similar.
Now let’s perform similar tests, but with log prices. Code is exactly the same, we just apply log function to the prices before trying to fit a model. Results are provided below.
Here approximately the same proportion of time series is identified as PAR. The average proportion of variance attributable to mean reversion is also similar — less than 50% for each time period. What about persistence?
Results of persistence tests also look very similar to the tests of normal price series. It seems that the PAR model works equally well for normal price series and for log price series. However, using this model in practice doesn't seem feasible because the proportion of variance attributable to mean reversion is too small — less than 50%. To use it for trading we need to further isolate the mean reversion component (e.g. using hedging), but this is a topic for another article.
In this article I explained the basic idea behind partial autoregressive model and implemented a function for estimating model parameters. We also performed several tests of the estimation procedure to make sure that everything works as expected.
Even though the model might not be very useful in its current form, it serves as a building block for a partial cointegration model that I will describe in the next article.
Jupyter notebook with source code is available here.
If you have any questions, suggestions or corrections please post them in the comments. Thanks for reading.
References
[2] Why I don’t like statistical tests
[3] AIC versus Likelihood Ratio Test in Model Variable Selection